Упр.292 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Решение #2 (Учебник 2023)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 7 класс, Просвещение:
Даны прямая а и отрезок АВ. Постройте прямую р, параллельную прямой а, так, чтобы расстояние между прямыми а и р было равно АВ.
Решение
Отметим на прямой а какую-нибудь точку С и проведём через точку С прямую b, перпендикулярную к прямой а (рис. 142). Затем на одном из лучей прямой b, исходящих из точки С, отложим отрезок CD, равный отрезку АВ. Через точку D проведём прямую р, перпендикулярную к прямой b. Прямая р — искомая (объясните почему). Как видно из построения, для любой данной прямой а и любого данного отрезка АВ искомую прямую можно построить, причём задача имеет два решения (прямые р и р1 на рисунке 143).
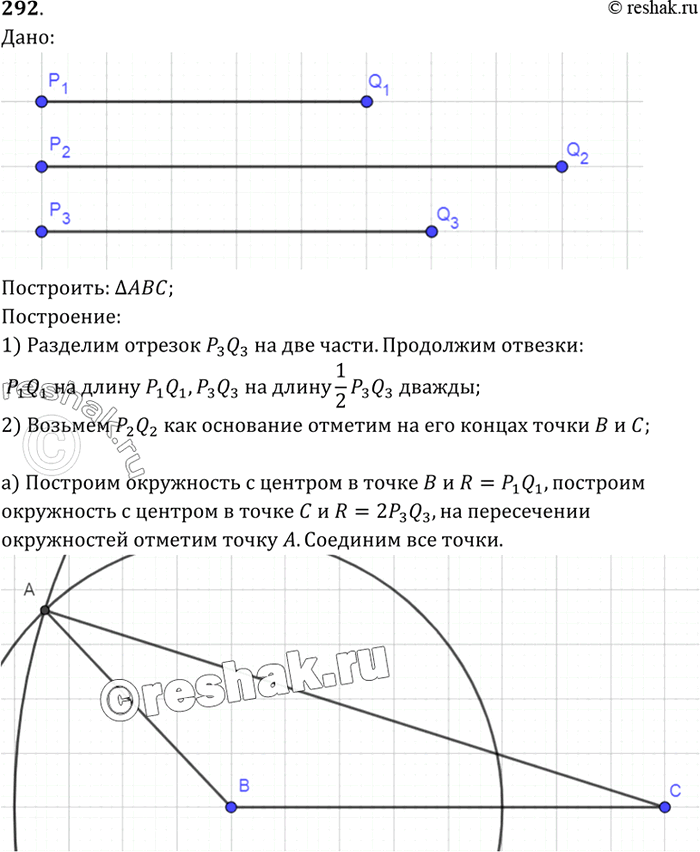
Даны отрезки P1Q1, P2Q2 и P3Q3 Постройте треугольник ABC так, чтобы:
а) AB =P1Q1, BC=P2Q2, CA = 2P3Q3,
б) AB = 2P1Ql, BC = P2Q2, CA = 3/2P3Q3.
Всегда ли задача имеет решение?
Похожие решебники
Популярные решебники 7 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением