Вопрос 3 Параграф 4 ГДЗ Погорелов 7-9 класс (Геометрия)
Решение #1
Рассмотрим вариант решения задания из учебника Погорелов 7 класс, Просвещение:
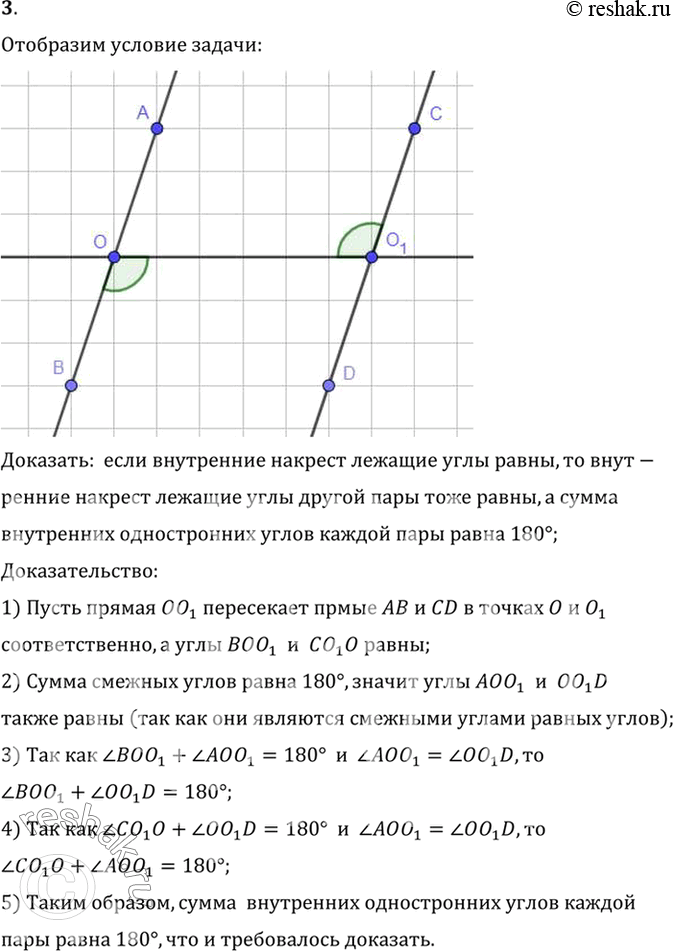
3. Докажите, что если внутренние накрест лежащие углы одной пары равны, то внутренние накрест лежащие углы другой пары тоже равны, а сумма внутренних односторонних углов каждой пары равна 180°.
Доказать: если внутренние накрест лежащие углы равны, то внут-
ренние накрест лежащие углы другой пары тоже равны, а сумма
внутренних одностронних углов каждой пары равна 180°;
Доказательство:
1) Пусть прямая OO1 пересекает прмые AB и CD в точках O и O1
соответственно, а углы BOO1 и CO1 O равны;
2) Сумма смежных углов равна 180°, значит углы AOO1 и OO1 D
также равны (так как они являются смежными углами равных углов);
3) Так как угол BOO1+ угол AOO1=180° и угол AOO1 = углу OO1 D, то
угол BOO1+ угол OO1 D=180°;
4) Так как угол CO1 O+ угол OO1 D=180° и угол AOO1 = углу OO1 D, то
угол CO1 O+ угол AOO1=180°;
5) Таким образом, сумма внутренних одностронних углов каждой
пары равна 180°, что и требовалось доказать.
Популярные решебники 7 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением





