Вопрос 12 Параграф 4 ГДЗ Погорелов 7-9 класс (Геометрия)
Решение #1
Рассмотрим вариант решения задания из учебника Погорелов 7 класс, Просвещение:
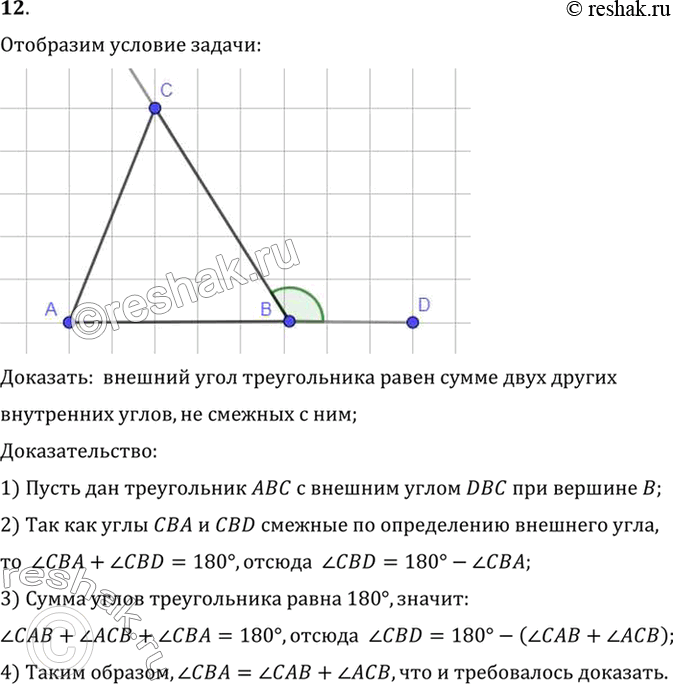
12. Докажите, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Доказать: внешний угол треугольника равен сумме двух других
внутренних углов, не смежных с ним;
Доказательство:
1) Пусть дан треугольник ABC с внешним углом DBC при вершине B;
2) Так как углы CBA и CBD смежные по определению внешнего угла,
то угол CBA+ угол CBD=180°, отсюда угол CBD=180°- угол CBA;
3) Сумма углов треугольника равна 180°, значит:
угол CAB+ угол ACB+ угол CBA=180°, отсюда угол CBD=180°-(угол CAB+ угол ACB);
4) Таким образом, угол CBA = углу CAB+ угол ACB, что и требовалось доказать.
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
