Упр.778 ГДЗ Мерзляк Полонский 5 класс (Математика)
Решение #1(Учебник 2026)
Решение #2(Учебник 2026)
Решение #3(Учебник 2019)
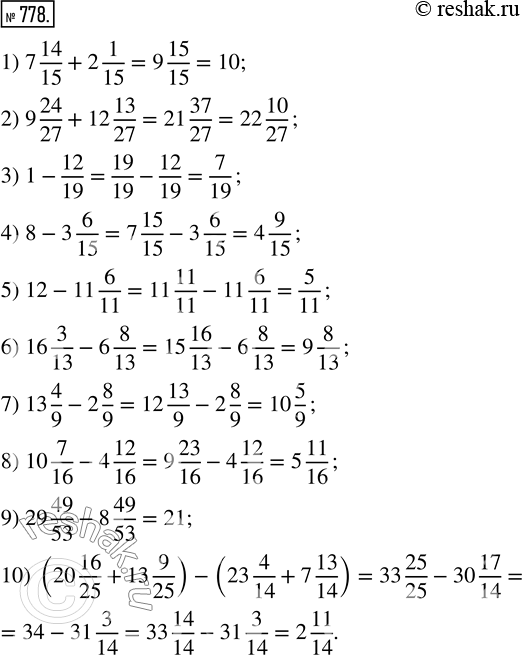
Решение #4(Учебник 2019)
Рассмотрим вариант решения задания из учебника
Мерзляк, Полонский, Якир 5 класс, Просвещение:
Задание учебника 2026 года
Найдите сумму длин всех рёбер и площадь поверхности куба, если его ребро равно 7 см.
Задание учебника 2019 года
Вычислите:
1) 7 14/15 + 2 1/15;
2) 9 24/27 + 12 13/27;
3) 1 - 12/19;
4) 8 - 3 6/15;
5) 12 - 11 6/11;
6) 16 3/13 - 6 8/13;
7) 13 4/9 - 2 8/9;
8) 10 7/16 - 4 12/16;
9) 29 49/53 - 8 49/53;
10) (20 16/25 + 13 9/25) - (23 4/14 + 7 13/14).
