Упр.498 ГДЗ Мерзляк Полонский 5 класс (Математика)
Решение #1 (Учебник 2024)
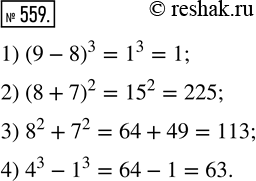
Решение #2 (Учебник 2024)



Решение #3 (Учебник 2019)

Решение #4 (Учебник 2019)



Рассмотрим вариант решения задания из учебника Мерзляк, Полонский, Якир 5 класс, Просвещение:
Составьте числовое выражение и найдите его значение:
1) куб разности чисел 9 и 8;
2) квадрат суммы чисел 8 и 7;
3) сумма квадратов чисел 8 и 7;
4) разность кубов чисел 4 и 1.
В равенстве a-b=c число a называют уменьшаемым, число b – вычитаемым, число c и запись a-b – разностью.
В равенстве a+b=c числа a и b называют слагаемыми, число c и запись a+b – суммой.
Степенью числа a с натуральным показателем n, большим 1, называется произведение n одинаковых множителей, каждый из которых равен числу a.
a•a•…•a=a^n
n множителей
Выражение a^n читают так: a в степени n или n-ная степень числа a и называют степенью.
При этом в этой записи число a называют основанием степени, а число n, которое показывает число множителей в произведении, - показателем степени.
Квадрат числа – это вторая степень числа.
Квадрат числа записывают так: a^2.
Куб числа – это третья степень числа.
Куб числа записывают так: a^3.
Стоит учитывать, что если в числовое выражение входит степень, то сначала выполняют возведение в степень, а потом остальные действия, в соответствии с порядком их выполнения, а именно:
1. Если необходимо выполнить только сложение и вычитание или только умножение и деление, то все действия выполняют по порядку слева направо.
2. Если необходимо выполнить несколько арифметических действий (сложение, вычитание, умножение и деление), то сначала выполняют умножение и деление по порядку слева направо, а затем сложение и вычитание по порядку слева направо.
3. Если в выражении есть скобки, то сначала выполняют действия в скобках, но обязательно учитывать правила, указанные выше.
1) Необходимо найти куб разности чисел 9 и 8.
Запишем разность чисел 9 и 8: 9-8.
Запишем куб получившейся разности чисел, то есть третью степень получившегося выражения.
Значит, основание степени равно 9-8, а показатель степени 3, то есть запишем (9-8)^3.
Далее решаем разность в скобках, записываем получившуюся степень в виде произведения, находим результат, то есть имеем:
(9-8)^3=1^3=1•1•1=1•1=1
2) Необходимо найти квадрат суммы чисел 8 и 7.
Запишем сумму чисел 8 и 7: 8+7.
Запишем квадрат получившейся суммы чисел, то есть вторую степень получившегося выражения.
Значит, основание степени равно 8+7, а показатель степени 2, то есть запишем (8+7)^2.
Далее находим значение выражения в скобках, записываем получившуюся степень в виде произведения, находим результат, то есть имеем:
(8+7)^2=15^2=15•15=225
3) Необходимо найти сумму квадратов чисел 8 и 7.
Запишем квадрат числа 8, то есть вторую степень числа 8.
Значит, основание степени равно 8, а показатель степени 2, то есть запишем 8^2.
Запишем квадрат числа 7, то есть вторую степень числа 7.
Значит, основание степени равно 7, а показатель степени 2, то есть запишем 7^2.
Сумму данных степеней запишем следующим образом: 8^2+7^2.
Далее записываем степени в виде произведений, находим их результат и складываем получившиеся значения, то есть имеем:
8^2+7^2=8•8+7•7=64+49=113
4) Необходимо найти разность кубов чисел 4 и 1.
Запишем куб числа 4, то есть третью степень числа 4.
Значит, основание степени равно 4, а показатель степени 3, то есть запишем 4^3.
Запишем куб числа 1, то есть третью степень числа 1.
Значит, основание степени равно 1, а показатель степени 3, то есть запишем 1^3.
Разность данных степеней запишем следующим образом: 4^3-1^3.
Далее записываем степени в виде произведений, находим их результат и вычитаем вычитаемое из уменьшаемого, то есть имеем:
4^3-1^3=4•4•4-1•1•1=16•4-1•1=64-1=63
Валентин подарил Виктории розы и орхидеи, причём орхидей было в 4 раза меньше, чем роз. Сколько роз подарил Валентин, если известно, что их было на 51 больше, чем орхидей?
Составим краткую запись условий задачи.
Розы ? шт, на 51 шт больше
Орхидеи ? шт, в 4 раза меньше
1 способ
Орхидеи составляют одну часть всех цветов, а розы – 4 такие же части.
Найдём, сколько цветов составляет одна часть.
Зная это, можно будет найти количество цветов каждого вида.
Известно, на сколько штук было больше роз (51), найдём эту разницу в частях.
Для этого надо вычесть количество частей роз (1) из количества частей орхидей (4).
4-1=3 (части) – на столько частей было больше роз.
51 цветок составляет 3 части.
Одна часть в 3 раза меньше, чем 51.
51:3=17 (шт) – одна часть, столько же было орхидей.
Розы составляют 4 такие части.
17•4=68 (шт) – было роз.
Ответ: 68 роз.
2 способ
Пусть орхидей было x шт. Тогда, роз было 4x шт.
По условию, если вычесть количество орхидей (x) из количества роз (4x), получится 51.
4x-x=51
При умножении на 1, число не меняется, поэтому x можно записать как 1•x.
4x-1•x=51
x - общий множитель уменьшаемого 4x и вычитаемого 1•x, вынесем его за скобки и найдём значение внутри скобок.
x•(4-1)=51
x•3=51
x - неизвестный множитель.
Для того, чтобы его найти, разделим произведение (51) на известный множитель (3).
x=51:3
x=17 (шт) – было орхидей.
4x=4•17=68 (шт) – было роз.
Ответ: 68 роз.
Похожие решебники
Популярные решебники 5 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







