Упр.3.107 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1
Решение #2
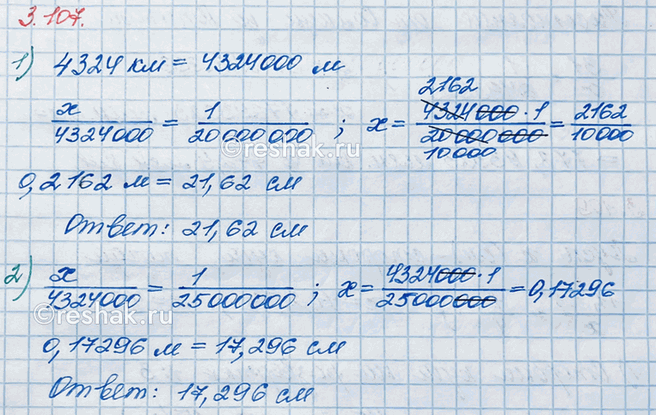
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
3.107. Длина Байкало-Амурской магистрали 4324 км. Какой длины получится линия, изображающая эту магистраль на карте, сделанной в масштабе:
1) 1 : 20 000 000; 2) 1 : 25 000 000?
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.
По условию длина Байкало-Амурской магистрали 4324 км.
Обозначим буквой x длину магистрали на карте в см.
Известно, что 1 км=1000 м=100 000 см, значит,
4 324 км=4 324•1 км=4 324•100 000 см=432 400 000 см.
Найдём отношение длины магистрали на карте к длине магистрали на местности, оно будет равно масштабу карты.
x:432 400 000 .
а) Масштаб карты равен 1:20 000 000 .
Составим пропорцию x:432 400 000=1:20 000 000 .
Произведение крайних членов пропорции равно произведению её средних членов, значит, x•20 000 000=1•432 400 000
x=(1•432 400 000)/(20 000 000) , так как чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель.
Выполнив сокращение в числителе и знаменателе выражения,
x=(100 000•2•2162)/(2•100 000•100)=21,62 см.
Ответ: 21,62 см.
б) Масштаб карты равен 1:25 000 000 .
Составим пропорцию x:432 400 000=1:25 000 000 .
x•25 000 000=1•432 400 000
x=(1•432 400 000)/(25 000 000)
x=(100 000•4324)/(100 000•250)=(4•4324)/(4•250)=17296/1000=17,296 см.
Ответ: 17,296 см.
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
