Упр.2.96 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
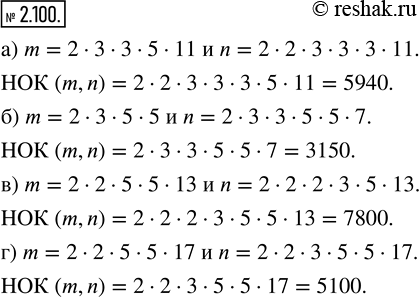
Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)
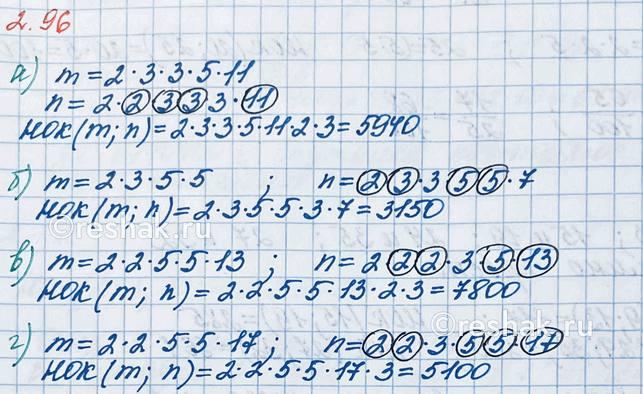
Решение #4 (Учебник 2021)
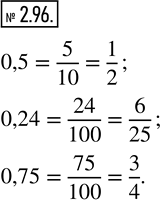
Решение #5 (Учебник 2021)

Решение #6 (Учебник 2021)
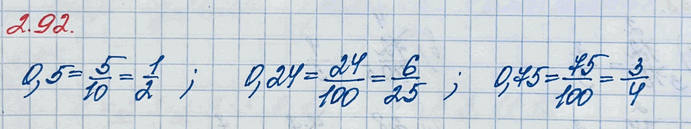
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите НОК (m, n), если:
а) m = 2 · 3 · 3 · 5 · 11 и n = 2 · 2 · 3 · 3 · 3 · 11;
б) m = 2 · 3 · 5 · 5 и n = 2 · 3 · 3 · 5 · 5 · 7;
в) m = 2 · 2 · 5 · 5 · 13 и n = 2 · 2 · 2 · 3 · 5 · 13;
г) m = 2 · 2 · 5 · 5 · 17 и n = 2 · 2 · 3 · 5 · 5 · 17.
Наименьшим общим кратным (НОК) натуральных чисел a и b называют наименьшее натуральное число, которое кратно и a,и b (делится и на a,и на b).
Для того, чтобы найти наименьшее общее кратное (НОК) чисел, необходимо:
- разложить их на простые множители;
- выписать множители, входящие в разложение одного из чисел;
- добавить к ним недостающие множители из разложения второго числа;
- найти значение получившегося произведения.
а) m=2•3•3•5•11,n=2•2•3•3•3•11
НОК(m; n)=2•3•3•5•11•2•3=10•9•22•3=270•22=
=5 940
б) m=2•3•5•5,n=2•3•3•5•5•7
НОК(m; n)=2•3•5•5•3•7=50•9•7=50•63=3 150
в) m=2•2•5•5•13,n=2•2•2•3•5•13
НОК(m; n)=2•2•5•5•13•2•3=100•13•6=100•78=
=7 800
г) m=2•2•5•5•17,n=2•2•3•5•5•17
НОК(m; n)=2•2•5•5•17•3=100•51=5 100
Запишите в виде обыкновенной дроби числа 0,5; 0,24: 0,75.
При переводе десятичной дроби (например, 0,5) в обыкновенную, в числителе дроби записывают число, стоящее после запятой (5), а в знаменателе 1 с таким количеством нулей, сколько знаков после запятой в десятичной дроби (10).
0,5=5/10
Если числитель и знаменатель дроби 5/10 разделить на одно и то же натуральное число (в данном случае на 5), то получится равная ей дробь.
5/10=(5:5)/(10:5)=1/2
Таким образом, 0,5=5/10=1/2 .
Десятичные дроби 0,24 и 0,75 переводим в обыкновенные аналогично.
0,24=24/100=(24:4)/(100:4)=6/25
0,75=75/100=(75:25)/(100:25)=3/4
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









