Упр.2.397 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
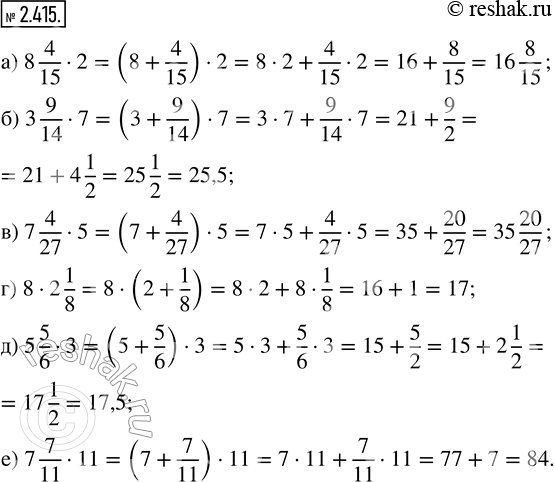
Решение #2 (Учебник 2023)
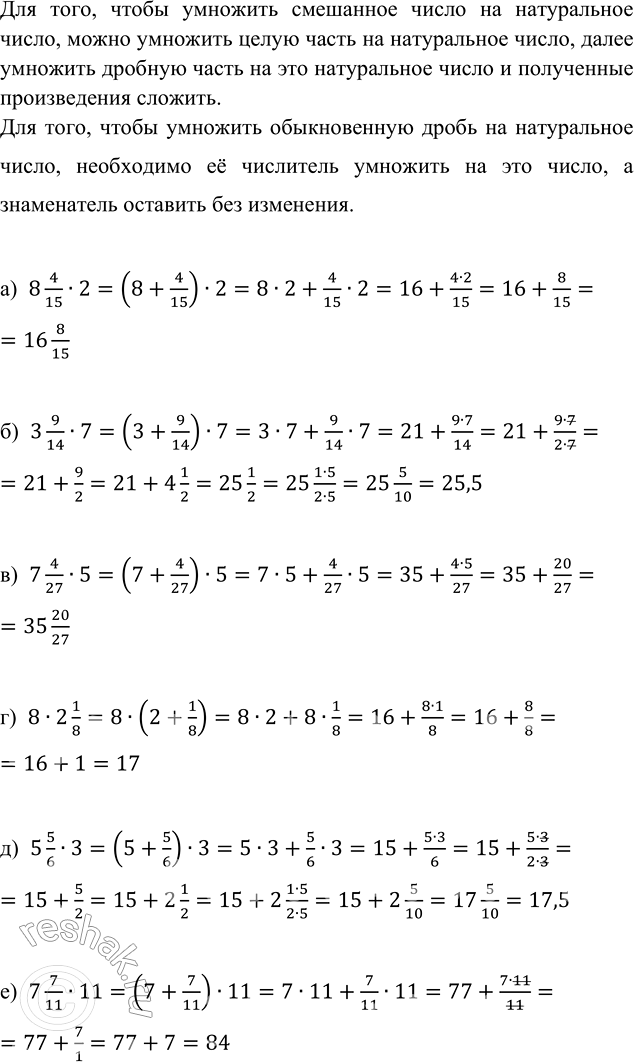
Решение #3 (Учебник 2023)
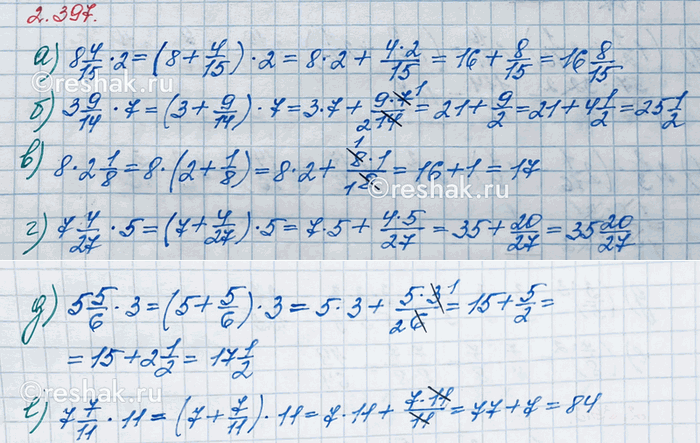
Решение #4 (Учебник 2021)
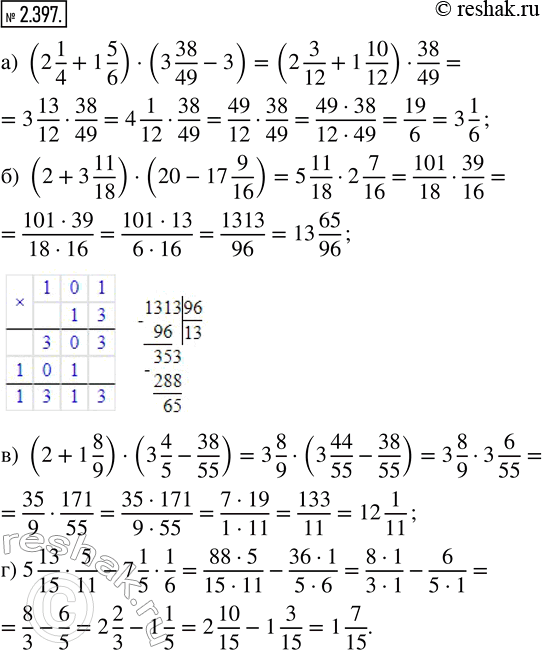
Решение #5 (Учебник 2021)
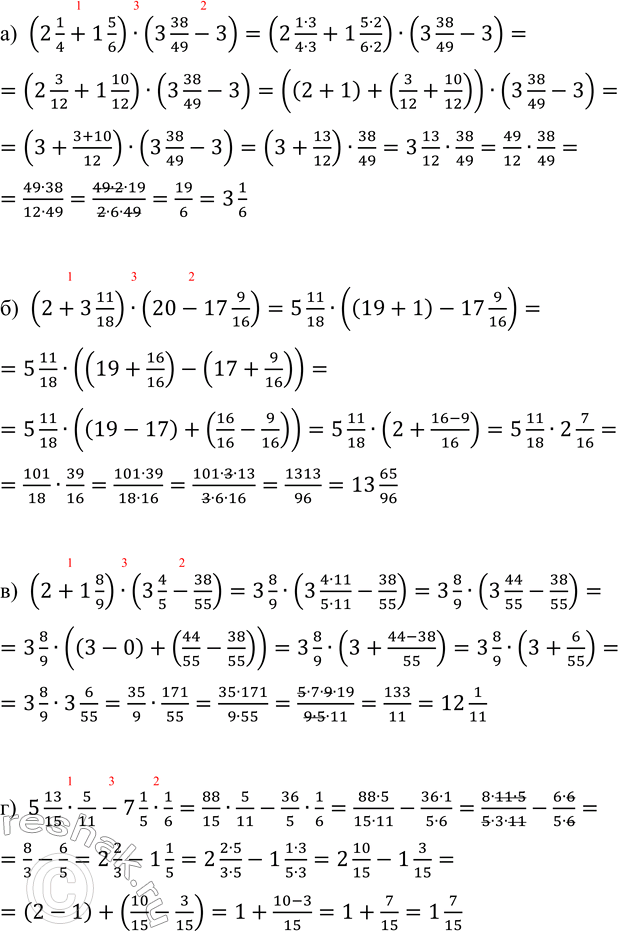
Решение #6 (Учебник 2021)
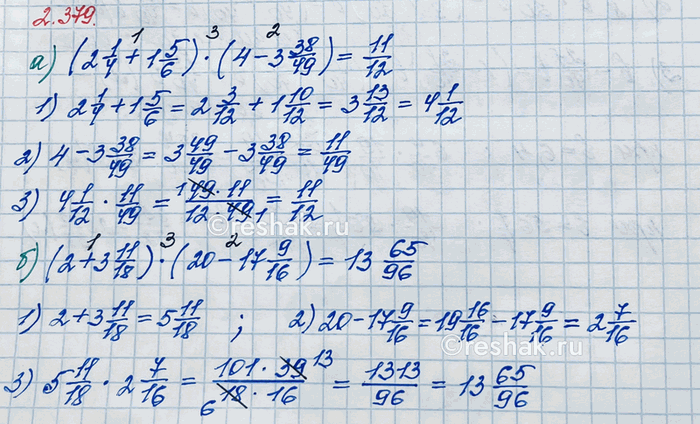
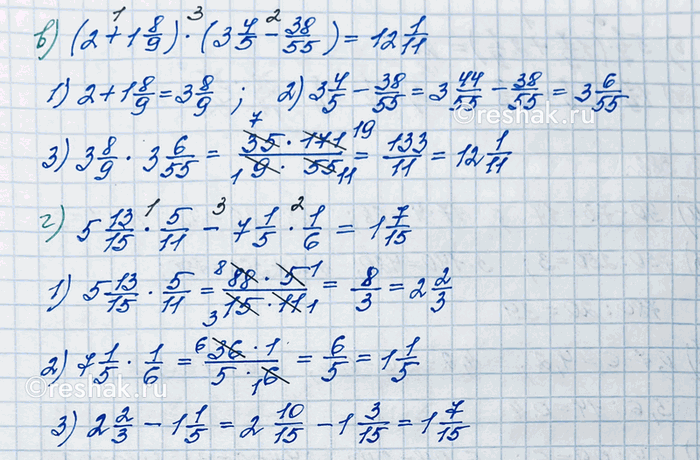
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите произведение:
а) 8 4/15 · 2; б) 3 9/14 · 7; в) 7 4/27 · 5; г) 8 · 2 1/8; д) 5 5/6 · 3; е) 7 7/11 · 11.
Для того, чтобы умножить смешанное число на натуральное число, можно умножить целую часть на натуральное число, далее умножить дробную часть на это натуральное число и полученные произведения сложить.
Для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменения.
а) 8 4/15•2=(8+4/15)•2=8•2+4/15•2=16+(4•2)/15=16+8/15=16 8/15
б) 3 9/14•7=(3+9/14)•7=3•7+9/14•7=21+(9•7)/14=21+(9•7)/(2•7)=21+9/2=21+4 1/2=25 1/2=25 (1•5)/(2•5)=25 5/10=25,5
в) 7 4/27•5=(7+4/27)•5=7•5+4/27•5=35+(4•5)/27=35+20/27=35 20/27
г) 8•2 1/8=8•(2+1/8)=8•2+8•1/8=16+(8•1)/8=16+8/8=16+1=17
д) 5 5/6•3=(5+5/6)•3=5•3+5/6•3=15+(5•3)/6=15+(5•3)/(2•3)=15+5/2=15+2 1/2=15+2 (1•5)/(2•5)=15+2 5/10=17 5/10=17,5
е) 7 7/11•11=(7+7/11)•11=7•11+7/11•11=77+(7•11)/11=77+7/1=77+7=84
Найдите значение выражения:
а) (2 1/4 + 1 5/6) · (3 - 3 38/49); в) (2 + 1 8/9) · (3 4/5 - 38/55);
6) (2 + 3 11/18) · (20 - 17 9/16); г) 5 13/15 · 5/11 - 7 1/5 · 1/6.
Для того, чтобы выполнить сложение (вычитание) смешанных чисел, необходимо дробные части привести к общему знаменателю, затем отдельно выполнить сложение (вычитание) целых частей и дробных частей.
При умножении числителя и знаменателя дроби на одно и то же число, получается дробь равная данной.
При сложении (вычитании) дробей с одинаковыми знаменателями, их числители складывают, а знаменатель оставляют тот же.
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
Смешанные числа перед умножением необходимо представить в виде неправильных дробей.
Для того, чтобы записать смешанное число в виде неправильной дроби, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
При этом, прежде, чем перемножить числа, выполняем сокращение.
а) (2 1/4+1 5/6)•(3 38/49-3)=(2 (1•3)/(4•3)+1 (5•2)/(6•2))•(3 38/49-3)=(2 3/12+1 10/12)•(3 38/49-3)=((2+1)+(3/12+10/12))•(3 38/49-3)=(3+(3+10)/12)•(3 38/49-3)=(3+13/12)•38/49=3 13/12•38/49=49/12•38/49=(49•38)/(12•49)=(49•2•19)/(2•6•49)=19/6=3 1/6
б) (2+3 11/18)•(20-17 9/16)=5 11/18•((19+1)-17 9/16)=5 11/18•((19+16/16)-(17+9/16))=5 11/18•((19-17)+(16/16-9/16))=5 11/18•(2+(16-9)/16)=5 11/18•2 7/16=101/18•39/16=(101•39)/(18•16)=(101•3•13)/(3•6•16)=1313/96=13 65/96
в) (2+1 8/9)•(3 4/5-38/55)=3 8/9•(3 (4•11)/(5•11)-38/55)=3 8/9•(3 44/55-38/55)=3 8/9•((3-0)+(44/55-38/55))=3 8/9•(3+(44-38)/55)=3 8/9•(3+6/55)=3 8/9•3 6/55=35/9•171/55=(35•171)/(9•55)=(5•7•9•19)/(9•5•11)=133/11=12 1/11
г) 5 13/15•5/11-7 1/5•1/6=88/15•5/11-36/5•1/6=(88•5)/(15•11)-(36•1)/(5•6)=(8•11•5)/(5•3•11)-(6•6)/(5•6)=8/3-6/5=2 2/3-1 1/5=2 (2•5)/(3•5)-1 (1•3)/(5•3)=2 10/15-1 3/15=(2-1)+(10/15-3/15)=1+(10-3)/15=1+7/15=1 7/15
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением