Упр.2.395 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
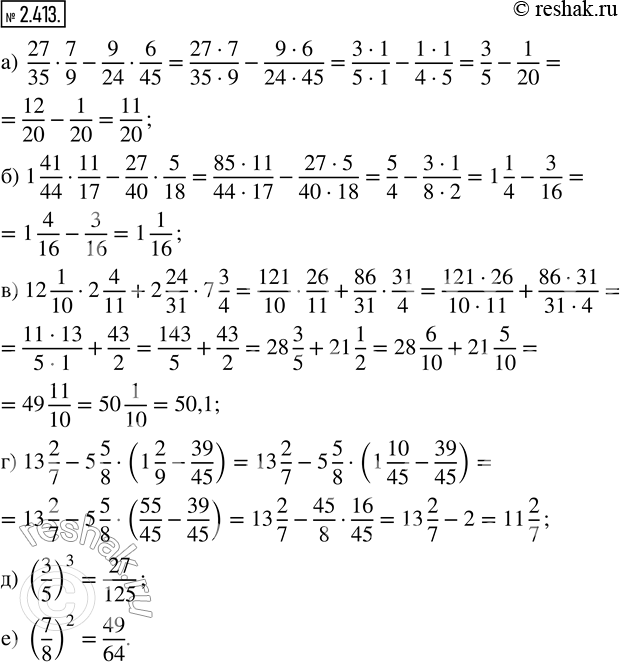
Решение #2 (Учебник 2023)

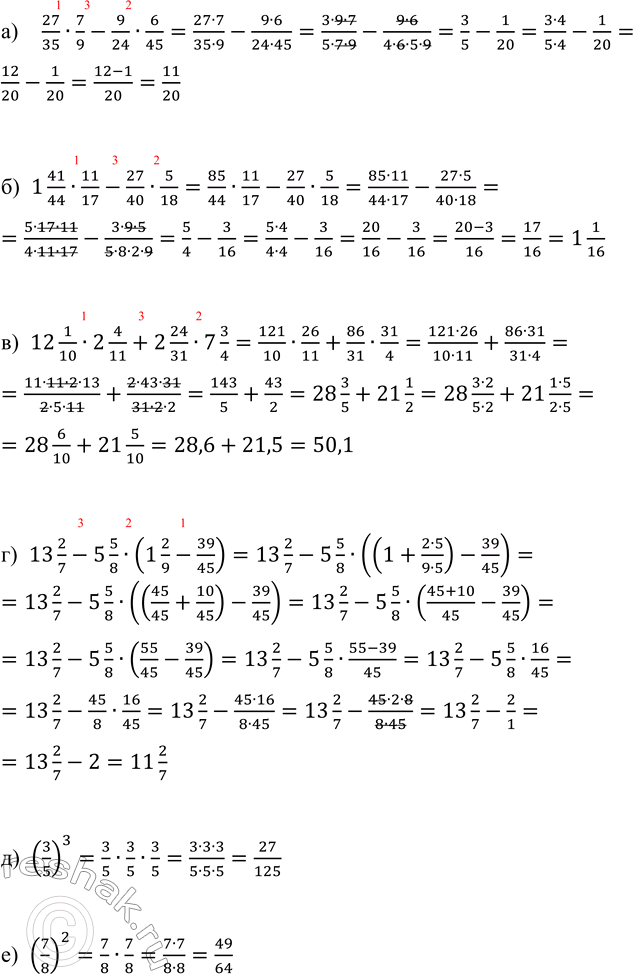
Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Выполните действия:
а) 27/35 · 7/9 - 9/24 · 6/45; в) 12 1/10 · 2 4/11 + 2 24/31 · 7 3/4; д) (3/5)^3;
б) 1 41/44 · 11/17 - 27/40 · 5/18; г) 13 2/7 - 5 5/8 · (1 2/9 - 39/45); е) (7/8)^2.
Если в выражении есть скобки, то сначала выполняют действия в скобках.
Если выражение содержит действия первой и второй ступени, то сначала выполняют действия второй ступени по порядку слева направо, а потом действия первой ступени, также по порядку слева направо.
При этом сложение и вычитание чисел называют действиями первой ступени, а умножение и деление чисел – действиями второй ступени.
При выполнении вычислений опираемся на следующие правила:
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
- для того, чтобы выполнить умножение смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
- для того, чтобы записать смешанное число в виде неправильной дроби, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
- для того, чтобы сложить (вычесть) дроби с разными знаменателями, необходимо сначала привести эти дроби к наименьшему общему знаменателю (используя дополнительные множители), а затем сложить (вычесть) их числители, а знаменатель оставить прежним.
Прежде, чем перемножать числа, сокращаем их.
а) 27/35•7/9-9/24•6/45=(27•7)/(35•9)-(9•6)/(24•45)=(3•9•7)/(5•7•9)-(9•6)/(4•6•5•9)=3/5-1/20=(3•4)/(5•4)-1/20=12/20-1/20=(12-1)/20=11/20
б) 1 41/44•11/17-27/40•5/18=85/44•11/17-27/40•5/18=(85•11)/(44•17)-(27•5)/(40•18)=(5•17•11)/(4•11•17)-(3•9•5)/(5•8•2•9)=5/4-3/16=(5•4)/(4•4)-3/16=20/16-3/16=(20-3)/16=17/16=1 1/16
в) 12 1/10•2 4/11+2 24/31•7 3/4=121/10•26/11+86/31•31/4=(121•26)/(10•11)+(86•31)/(31•4)=(11•11•2•13)/(2•5•11)+(2•43•31)/(31•2•2)=143/5+43/2=28 3/5+21 1/2=28 (3•2)/(5•2)+21 (1•5)/(2•5)=28 6/10+21 5/10=28,6+21,5=50,1
г) 13 2/7-5 5/8•(1 2/9-39/45)=13 2/7-5 5/8•((1+(2•5)/(9•5))-39/45)=13 2/7-5 5/8•((45/45+10/45)-39/45)=13 2/7-5 5/8•((45+10)/45-39/45)=13 2/7-5 5/8•(55/45-39/45)=13 2/7-5 5/8•(55-39)/45=13 2/7-5 5/8•16/45=13 2/7-45/8•16/45=13 2/7-(45•16)/(8•45)=13 2/7-(45•2•8)/(8•45)=13 2/7-2/1=13 2/7-2=11 2/7
д) (3/5)^3=3/5•3/5•3/5=(3•3•3)/(5•5•5)=27/125
е) (7/8)^2=7/8•7/8=(7•7)/(8•8)=49/64
На заправке было b тыс. л бензина. В первый день продали 7/8 этого бензина, во второй — 0,4 того количества, которое продали в первый день. Сколько бензина осталось на заправке? Найдите значение получившегося выражения при b = 4,5; b = 56 1/4.
Для того, чтобы найти часть от числа, выраженную обыкновенной или десятичной дробью, необходимо умножить число на эту дробь.
По условию, в первый день продали 7/8 всего бензина, значит, чтобы найти количество бензина, проданного в первый день, необходимо 7/8 умножить на количество бензина, которое было на заправке b, то есть в первый день продали 7/8 b тыс.л бензина.
Во второй день продали 0,4 того количества бензина, которое продали в первый день, значит, чтобы найти количество бензина, проданного во второй день, необходимо 0,4 умножить на количество бензина, проданного в первый день 7/8 b, то есть во второй день продали
7/8 b•0,4=7/8 b•4/10=(7•4)/(8•10) b=(7•4)/(4•2•10) b=7/20 b=(7•5)/(20•5) b=35/100 b=0,35b (тыс.л).
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель - произведению знаменателей.
Тогда, за два дня продали 7/8 b+0,35b=(7•125)/(8•125) b+0,35b=
=875/1000 b+0,35b=0,875b+0,35b=1,225b(тыс.л) – бензина.
Тогда, на заправке должно остаться
b-1,225b=(1-1,225)b<0
Таким образом, получается, что продали бензина больше, чем его было на заправке первоначально, что невозможно.
Поэтому, задача не имеет смысла ни при каком значении b.
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.