Упр.2.366 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
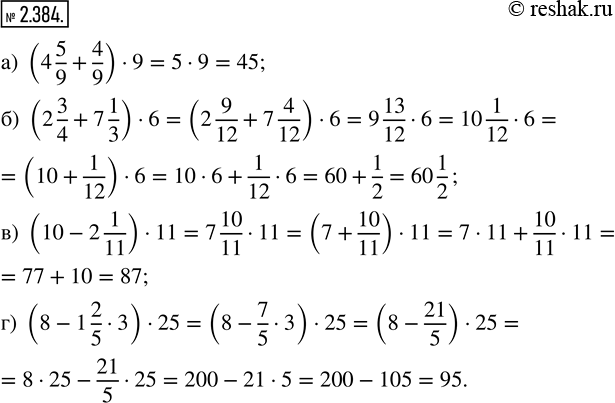
Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)

Решение #5 (Учебник 2021)



Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Найдите значение выражения:
а) (4 5/9 + 4/9) · 9; б) (2 3/4 + 7 1/3) · 6; в) (10 - 2 1/11) · 11; г) (8 - 1 2/5 · 3) · 25.
Используем распределительное свойство умножения относительно сложения.
Для того, чтобы умножить смешанное число на натуральное число, можно умножить целую часть на натуральное число; умножить дробную часть на это натуральное число; затем сложить полученные результаты.
Для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменений.
Прежде, чем выполнить умножение, выполняем сокращение дробей (если это возможно), то есть делим числитель и знаменатель на одно и то же число (наибольший общий делитель).
Дробь, у которой в знаменателе стоит единица, равна числителю.
Для того, чтобы выполнить сложение (вычитание) смешанных чисел, необходимо дробные части привести к общему знаменателю, затем отдельно выполнить сложение (вычитание) целых частей и дробных частей.
При умножении числителя и знаменателя дроби на одно и то же число, получается дробь равная данной.
При сложении (вычитании) дробей с одинаковыми знаменателями, их числители складывают, а знаменатель оставляют тот же.
а) (4 5/9+4/9)•9=((4+0)+(5/9+4/9))•9=(4+(5+4)/9)•9=(4+9/9)•9=(4+1)•9=5•9=45
б) (2 3/4+7 1/3)•6=(2 (3•3)/(4•3)+7 (1•4)/(3•4))•6=(2 9/12+7 4/12)•6=((2+7)+(9/12+4/12))•6\=(9+(9+4)/12)•6=(9+13/12)•6=(9+1 1/12)•6=(10+1/12)•6=10•6+1/12•6=60+6/12=60+(6•1)/(6•2)=60+1/2=60 1/2
в) (10-2 1/11)•11=((9+1)-2 1/11)•11=((9+11/11)-(2+1/11))•11=((9-2)+(11/11-1/11))•11=(7+(11-1)/11)•11=(7+10/11)•11=7•11+10/11•11=77+(10•11)/11==77+10/1=77+10=87
г) (8-1 2/5•3)•25=(8-7/5•3)•25=(8-(7•3)/5)•25=(8-21/5)•25=8•25-21/5•25=200-(21•25)/5=200-(21•5•5)/5=200-105/1=200-105=95
) Для освещения площади используют 29 фонарей, в которых три или две лампочки. Сколько фонарей каждого вида на площади, если всего лампочек 76?
Решаем задачу с помощью уравнения.
Для освещения площади используют 29 фонарей двух видов – с двумя и с тремя лампочками.
Пусть x – число фонарей с двумя лампочками, тогда 29-x – число фонарей с тремя лампочками.
Значит, имеется x фонарей, в которых по две лампочки, значит, всего у этих фонарей 2x лампочек, и 29-x фонарей с тремя лампочками, значит, всего у этих фонарей 3•(29-x) лампочек.
При этом вместе у всех фонарей 76 лампочек.
Следовательно, можно составить следующее уравнение:
2x+3•(29-x)=76 или, используя распределительное свойство умножения относительно вычитания, то есть раскрываем скобки, умножив каждый компонент, стоящий в скобках, на 3, получим 2x+87-3x=76 .
Далее используем свойство вычитания, согласно которому, чтобы к разности чисел прибавить натуральное число, можно сначала прибавить это число к уменьшаемому, а затем отнять от полученной суммы вычитаемое, получим
87+2x-3x=76
Далее используем распределительное свойство умножения относительно вычитания, то есть выносим одинаковый множитель x за скобки, получим
87+(2-3)x=76 , или, выполнив вычитание в скобках,
87+(-1)x=76
При умножении единицы на любое число, получим равное ему число, тогда можно записать
87-x=76
В полученном уравнении неизвестно вычитаемое x.
Для того, чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность, получим
x=87-76 или, выполнив вычитание,
x=11
Значит, с двумя лампочками было 11 фонарей.
Тогда, с тремя лампочками было
29-x=29-11=18 (фонарей).
Ответ: 11 фонарей с двумя лампочками; 18 фонарей с тремя лампочками.
2) К новогоднему празднику для 23 детей купили машинки с тремя и с четырьмя колёсами. Сколько машинок каждого вида было куплено, если всего колёс 83?
Решаем задачу с помощью уравнения.
К новогоднему празднику купили 23 машинки двух видов – с тремя и с четырьмя колёсами.
Пусть x – число машинок с тремя колёсами, тогда 23-x – число машинок с четырьмя колёсами.
Значит, имеется x машинок, у которых по 3 колеса, значит, всего у этих машинок 3x колёс, и 23-x машинки, у которых по 4 колеса, значит, всего у этих машинок 4•(23-x) колеса.
При этом вместе у всех машинок 83 колеса.
Следовательно, можно составить следующее уравнение:
3x+4•(23-x)=83 или, используя распределительное свойство умножения относительно вычитания, то есть раскрываем скобки, умножив каждый компонент, стоящий в скобках, на 4, получим 3x+92-4x=83 .
Далее используем свойство вычитания, согласно которому, чтобы к разности чисел прибавить натуральное число, можно сначала прибавить это число к уменьшаемому, а затем отнять от полученной суммы вычитаемое, получим
92+3x-4x=83
Далее используем распределительное свойство умножения относительно вычитания, то есть выносим одинаковый множитель x за скобки, получим
92+(3-4)x=83 , или, выполнив вычитание в скобках,
92+(-1)x=83
При умножении единицы на любое число, получим равное ему число, тогда можно записать
92-x=83
В полученном уравнении неизвестно вычитаемое x.
Для того, чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность, получим
x=92-83 или, выполнив вычитание,
x=9
Значит, с тремя колёсами было 9 машинок.
Тогда, с четырьмя колёсами было
23-x=23-9=14 (машинок).
Ответ: 9 машинок с тремя колёсами; 14 машинок с четырьмя колёсами.
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









