Упр.2.148 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)



Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)
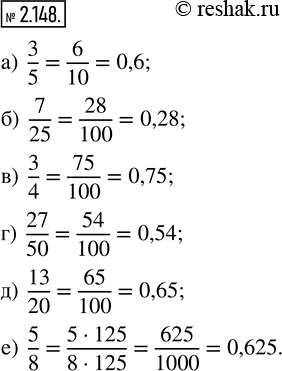
Решение #5 (Учебник 2021)



Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Какая из дробей больше:
а) 5/6 или 23/24; б) 6/11 или 10/19; в) 7/30 или 3/10; г) 4/35 или 5/21?
а) 5/6 и 23/24
Для того, чтобы сравнить дроби с разными знаменателями, необходимо привести данные дроби к наименьшему общему знаменателю.
Для этого необходимо определить для чисел 6 и 24 их наименьшее общее кратное (НОК).
6=2•3
24=2•2•2•3
Для того, чтобы определить НОК, необходимо недостающие множители (в данном случае их нет) добавить к множителям большего числа и перемножить их:
НОК(6,24)=2•2•2•3=24
Далее определим дополнительный множитель для дроби 5/6 .
24:6=4 – дополнительный множитель для дроби 5/6 .
5/6=(5•4)/(6•4)=20/24
Теперь сравниваем дроби 20/24 и 23/24 .
Так как 20<23, значит, 20/24<23/24
Таким образом, 5/6<23/24
б) 6/11 и 10/19
Для того, чтобы сравнить дроби с разными знаменателями, необходимо привести данные дроби к наименьшему общему знаменателю.
Для этого необходимо определить для чисел 11 и 19 их наименьшее общее кратное (НОК). Оба числа простые.
Для того, чтобы определить НОК, необходимо недостающие множители (в данном случае их нет) добавить к множителям большего числа и перемножить их:
НОК(11,19)=11•19=209
Далее определим дополнительные множители для дробей 6/11 и 10/19
209:11=19 – дополнительный множитель для дроби 6/11 .
6/11=(6•19)/(11•19)=114/209
209:19=11 – дополнительный множитель для дроби 10/19 .
10/19=(10•11)/(19•11)=110/209
Теперь сравниваем дроби 114/209 и 110/209 .
Так как 114>110, значит, 114/209>110/209
Таким образом, 6/11>10/19
в) 7/30 и 3/10
Для того, чтобы сравнить дроби с разными знаменателями, необходимо привести данные дроби к наименьшему общему знаменателю.
Для этого необходимо определить для чисел 30 и 10 их наименьшее общее кратное (НОК).
30=2•3•5
10=2•5
Для того, чтобы определить НОК, необходимо недостающие множители (в данном случае их нет) добавить к множителям большего числа и перемножить их:
НОК(10,30)=2•3•5=30
Далее определим дополнительный множитель для дроби 3/10 .
30:10=3 – дополнительный множитель для дроби 3/10 .
3/10=(3•3)/(10•3)=9/30
Теперь сравниваем дроби 7/30 и 9/30 .
Так как 7<9, значит, 7/30<9/30
Таким образом, 7/30<3/10
г) 4/35 и 5/21
Для того, чтобы сравнить дроби с разными знаменателями, необходимо привести данные дроби к наименьшему общему знаменателю.
Для этого необходимо определить для чисел 35 и 21 их наименьшее общее кратное (НОК).
35=5•7
21=3•7
Для того, чтобы определить НОК, необходимо недостающие множители (выделен цветом) добавить к множителям большего числа и перемножить их:
НОК(21,35)=3•5•7=105
Далее определим дополнительные множители для дробей 4/35 и 5/21
105:35=3 – дополнительный множитель для дроби 4/35 .
4/35=(4•3)/(35•3)=12/105
105:21=5 – дополнительный множитель для дроби 5/21 .
5/21=(5•5)/(21•5)=25/105
Теперь сравниваем дроби 12/105 и 25/105 .
Так как 12<25, значит, 12/105<25/105 , то есть 4/35<5/21 .
Запишите в виде десятичной дроби:
а) 3/5; б) 7/25; в) 3/4; г) 27/50; д) 13/20; е) 5/8.
а) Для того, чтобы дробь 3/5 представить в виде десятичной дроби, сначала расширяем эту дробь на число 2 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 10.
3/5=(3•2)/(5•2)=6/10
Дробь 6/10 можно записать без знаменателя ( в виде десятичной дроби).
Сначала пишем целую часть (0), а потом числитель дробной части (6).
Целую часть отделяем от дробной части запятой.
6/10=0,6
б) Для того, чтобы дробь 7/25 представить в виде десятичной дроби, сначала расширяем эту дробь на число 4 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 100.
7/25=(7•4)/(25•4)=28/100
Дробь 28/100 можно записать без знаменателя ( в виде десятичной дроби).
Сначала пишем целую часть (0), а потом числитель дробной части (28).
Целую часть отделяем от дробной части запятой.
28/100=0,28
в) Для того, чтобы дробь 3/4 представить в виде десятичной дроби, сначала расширяем эту дробь на число 25 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 100.
3/4=(3•25)/(4•25)=75/100
Дробь 75/100 можно записать без знаменателя ( в виде десятичной дроби).
Сначала пишем целую часть (0), а потом числитель дробной части (75).
Целую часть отделяем от дробной части запятой.
75/100=0,75
г) Для того, чтобы дробь 27/50 представить в виде десятичной дроби, сначала расширяем эту дробь на число 2 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 100.
27/50=(27•2)/(50•2)=54/100
Дробь 54/100 можно записать без знаменателя ( в виде десятичной дроби).
Сначала пишем целую часть (0), а потом числитель дробной части (54).
Целую часть отделяем от дробной части запятой.
54/100=0,54
д) Для того, чтобы дробь 13/20 представить в виде десятичной дроби, сначала расширяем эту дробь на число 5 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 100.
13/20=(13•5)/(20•5)=65/100
Дробь 65/100 можно записать без знаменателя ( в виде десятичной дроби).
Сначала пишем целую часть (0), а потом числитель дробной части (65).
Целую часть отделяем от дробной части запятой.
65/100=0,65
е) Для того, чтобы дробь 5/8 представить в виде десятичной дроби, сначала расширяем эту дробь на число 125 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 1000.
5/8=(5•125)/(8•125)=625/1000
Дробь 625/1000 можно записать без знаменателя ( в виде десятичной дроби).
Сначала пишем целую часть (0), а потом числитель дробной части (625).
Целую часть отделяем от дробной части запятой.
625/1000=0,625
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.