Упр.2.117 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)



Решение #3 (Учебник 2023)
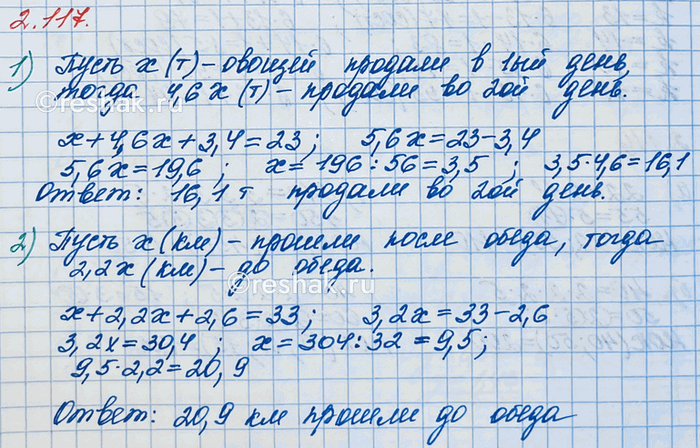
Решение #4 (Учебник 2021)
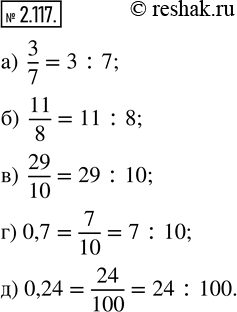
Решение #5 (Учебник 2021)


Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
) На овощной базе было 23 т овощей. В первый день продали в 4,6 раза меньше овощей, чем во второй день. К утру третьего дня на базе осталось 3,4 т овощей. Сколько тонн овощей продали во второй день?
Составим краткую запись условий задачи.
Первый день ? т, в 4,6 раза меньше
Второй день ? т 23 т
Третий день осталось 3,4 т
Пусть в первый день продали x т овощей.
Известно, что в первый день продали в 4,6 раза меньше овощей, чем во второй день. Значит, во второй день продали в 4,6 раза больше овощей, чем в первый день.
Тогда, во второй день продали 4,6x т овощей.
Зная, что к утру третьего дня на базе осталось 3,4 т овощей, по условию задачи составляем уравнение.
x+4,6x+3,4=23
Сумма двух слагаемых x и 4,6x в левой части уравнения равна 5,6x, потому что
x+4,6x=1x+4,6x=(1+4,6)x=5,6x (распределительный закон умножения относительно сложения).
Получим уравнение
5,6x+3,4=23
Неизвестно слагаемое 5,6x.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
5,6x=23-3,4
5,6x=19,6
Неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=19,6:5,6
x=3,5 (т) – овощей продали в первый день.
Для того, чтобы найти сколько овощей продали во второй день, необходимо в выражение 4,6x подставить значение x=3,5.
4,6x=4,6•3,5=16,1 (т) – овощей продали во второй день.
Ответ: 16,1 овощей.
2) Туристы запланировали пройти за день 33 км. До обеда они прошли в 2,2 раза большее расстояние, чем после обеда. К вечеру им осталось пройти 2,6 км. Сколько километров прошли туристы до обеда?
Составим краткую запись условий задачи.
До обеда ? км, в 2,2 раза больше
После обеда ? км 33 км
К вечеру осталось 2,6 км
Пусть после обеда туристы прошли x км.
Известно, что до обеда он прошли в 2,2 раза большее расстояние, чем после обеда.
Тогда, до обеда они прошли 2,2x км.
Зная, что к вечеру туристам осталось пройти 2,6 км, по условию задачи составляем уравнение.
x+2,2x+2,6=33
Сумма двух слагаемых x и 2,2x в левой части уравнения равна 3,2x, потому что
x+2,2x=1x+2,2x=(1+2,2)x=3,2x (распределительный закон умножения относительно сложения).
Получим уравнение
3,2x+2,6=33
Неизвестно слагаемое 3,2x.
Для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое, получим
3,2x=33-2,6
3,2x=30,4
Неизвестен множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=30,4:3,2
x=9,5 (км) – прошли туристы после обеда.
Для того, чтобы найти сколько туристы прошли до обеда, необходимо в выражение 2,2x подставить значение x=9,5.
2,2x=2,2•9,5=20,9 (км) – прошли туристы до обеда.
Ответ: 20,9 км.
Запишите в виде частного дробь:
а) 3/7; б) 11/8; в) 29/10; г) 0,7; д) 0,24.
Черту обыкновенной дроби можно понимать как знак деления, то есть a/b=a:b
а) 3/7=3:7
Числитель 3 является делимым.
Знаменатель 7 является делителем.
б) 11/8=11:8
Числитель 11 является делимым.
Знаменатель 8 является делителем.
в) 29/10=29:10
Числитель 29 является делимым.
Знаменатель 10 является делителем.
г) При переводе десятичной дроби (0,7) в обыкновенную в числителе дроби записывают число, стоящее после запятой (число 7), а разрядная единица в знаменателе содержит один ноль (столько знаков после запятой в десятичной дроби).
0,7=7/10
Тогда, решение будет записано так,
0,7=7/10=7:10
д) При переводе десятичной дроби (0,24) в обыкновенную в числителе дроби записывают число, стоящее после запятой (число 24), а разрядная единица в знаменателе содержит два нуля (столько знаков после запятой в десятичной дроби).
0,24=24/100
Тогда, решение будет записано так,
0,24=24/100=24:100
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









