Упр.13.29 ГДЗ Погорелов 7-9 класс (Геометрия)
Решение #1
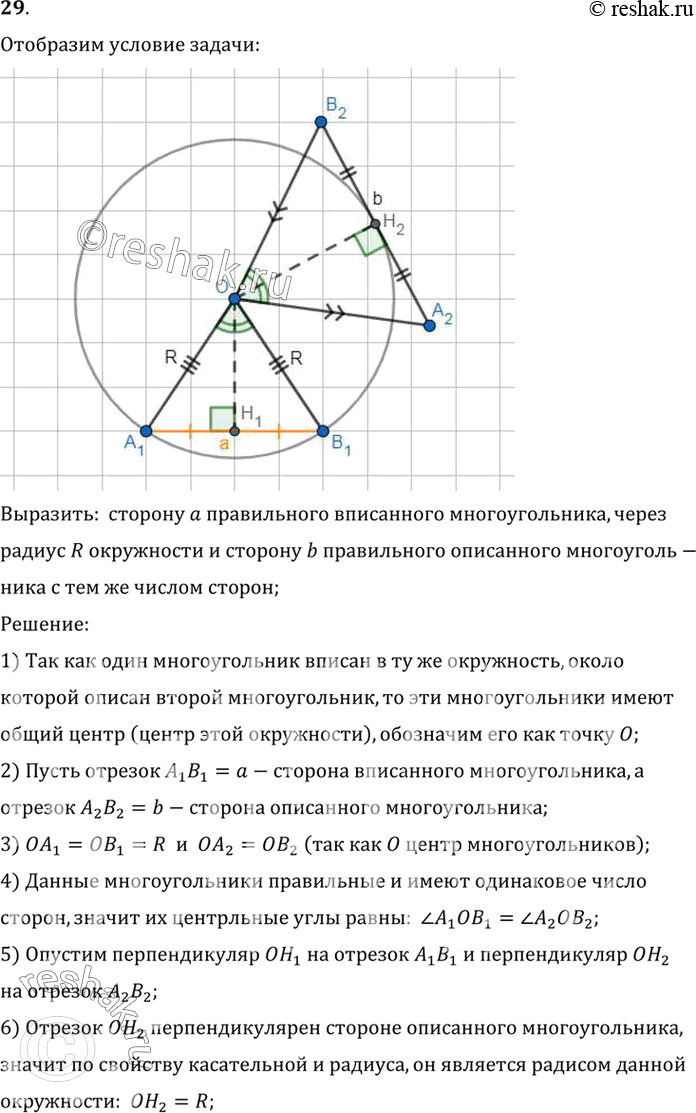
Рассмотрим вариант решения задания из учебника Погорелов 9 класс, Просвещение:
29. Выразите сторону а правильного вписанного многоугольника через радиус R окружности и сторону b правильного описанного многоугольника с тем же числом сторон.
Выразить: сторону a правильного вписанного многоугольника, через
радиус R окружности и сторону b правильного описанного многоуголь-
ника с тем же числом сторон;
Решение:
1) Так как один многоугольник вписан в ту же окружность, около
которой описан второй многоугольник, то эти многоугольники имеют
общий центр (центр этой окружности), обозначим его как точку O;
2) Пусть отрезок A1 B1=a-сторона вписанного многоугольника, а
отрезок A2 B2=b-сторона описанного многоугольника;
3) OA1=OB1=R и OA2=OB2 (так как O центр многоугольников);
4) Данные многоугольники правильные и имеют одинаковое число
сторон, значит их центрльные углы равны: угол A1 OB1 = углу A2 OB2;
5) Опустим перпендикуляр OH1 на отрезок A1 B1 и перпендикуляр OH2
на отрезок A2 B2;
6) Отрезок OH2 перпендикулярен стороне описанного многоугольника,
значит по свойству касательной и радиуса, он является радисом данной
окружности: OH2=R;
7) Треугольник OA2 B2-равнобедренный с основанием A2 B2, значит
его высота OH2 является медианой и биссектрисой, тогда:
A2 H2=1/2 A2 B2=b/2 и угол A2 OH2=1/2 угол A2 OB2;
8) Треугольник OA1 B1-равнобедренный с основанием A1 B1, значит
его высота OH1 является медианой и биссектрисой, тогда:
A1 H1=1/2 A1 B1=a/2 и угол A1 OH1=1/2 угол A1 OB1;
9) В прямоугольном треугольнике OH1 A1 по теореме Пифагора:
OH1=v(OA1^2-A1 H1^2)=v(R^2-(a/2)^2)=v(R^2-a^2/4);
10) Прямоугольные треугольники OH1 A1 и OH2 A2 подобны по острому
углу (угол A1 OH1 = углу A2 OH2)
Популярные решебники 9 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением