Упр.12.21 ГДЗ Погорелов 7-9 класс (Геометрия)
Решение #1
Рассмотрим вариант решения задания из учебника Погорелов 9 класс, Просвещение:
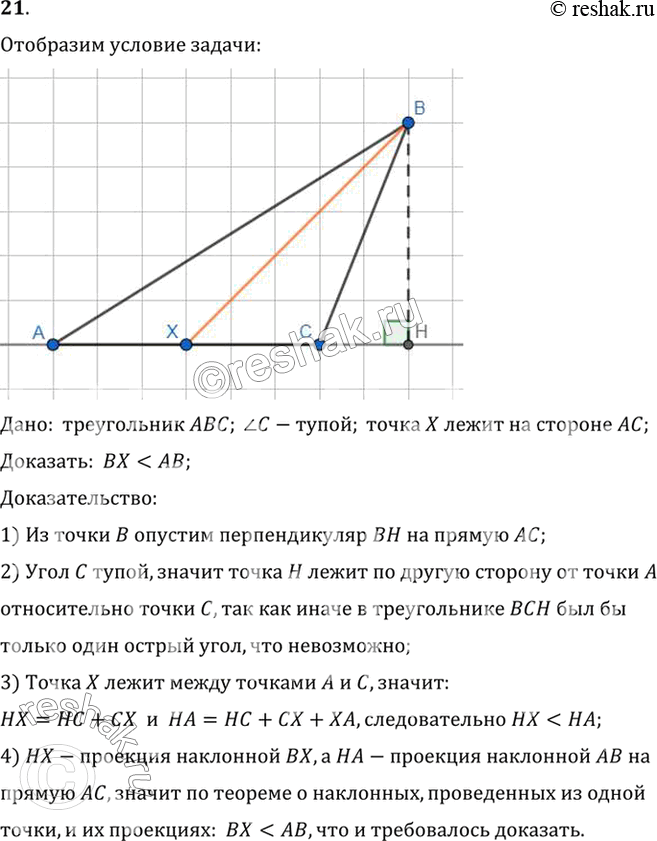
21. У треугольника ABC угол С тупой. Докажите, что если точка X лежит на стороне АС, то ВХ < АВ.
Дано: треугольник ABC; угол C-тупой; точка X лежит на стороне AC;
Доказать: BX
Доказательство:
1) Из точки B опустим перпендикуляр BH на прямую AC;
2) Угол C тупой, значит точка H лежит по другую сторону от точки A
относительно точки C, так как иначе в треугольнике BCH был бы
только один острый угол, что невозможно;
3) Точка X лежит между точками A и C, значит:
HX=HC+CX и HA=HC+CX+XA, следовательно HX
4) HX-проекция наклонной BX, а HA-проекция наклонной AB на
прямую AC, значит по теореме о наклонных, проведенных из одной
точки, и их проекциях: BX
Популярные решебники 9 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением