Упр.682 ГДЗ Макарычев Миндюк 9 класс (Алгебра)
Решение #1 (Учебник 2026)
Решение #2 (Учебник 2026)
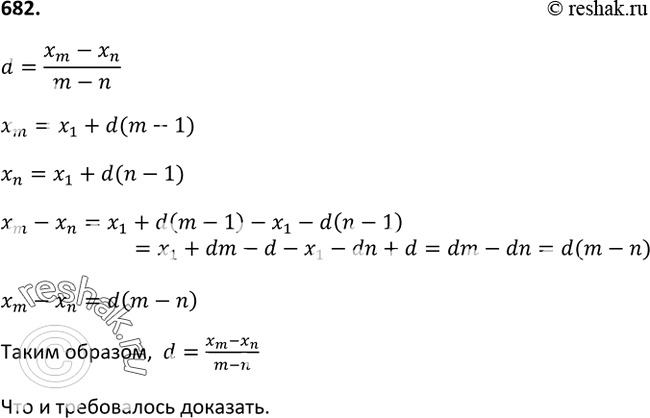
Решение #3 (Учебник 2026)
Решение #4 (Учебник 2024)
Решение #5 (Учебник 2024)
Решение #6 (Учебник 2024)
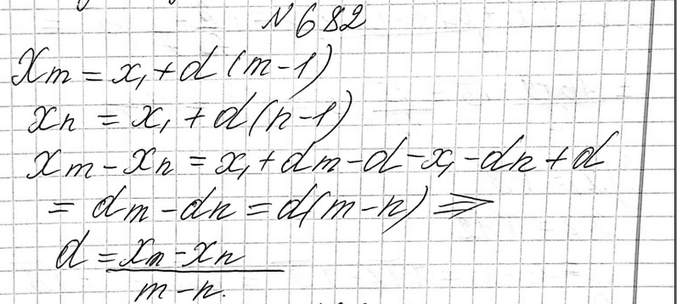
Рассмотрим вариант решения задания из учебника
Макарычев, Миндюк, Нешков 9 класс, Просвещение:
Задание учебника 2026 года
а) Телевизор стоил 10 ООО р. В апреле он подорожал на 30%, а в декабре подешевел на 40%. Сколько стал стоить телевизор в декабре?
б) Цену товара повысили на 30%, а через некоторое время снизили на 40%. На сколько процентов изменилась первоначальная цена товара?
Задание учебника 2024 года
Докажите, что если d — разность арифметической прогрессии, а хm и хn — члены этой прогрессии, причём m=/n, то d=(xm-xn)/(m-n).
