Упр.1357 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 9 класс, Просвещение:
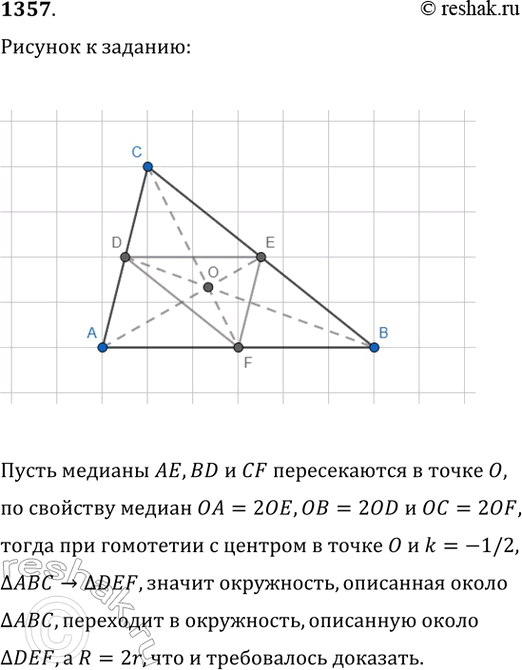
1357. Используя гомотетию с центром в точке пересечения медиан треугольника АВС, докажите, что радиус окружности, описанной около треугольника АВС, в 2 раза больше радиуса окружности, описанной около треугольника с вершинами в серединах сторон АВ, ВС и СА.
Пусть медианы AE,BD и CF пересекаются в точке O, по свойству медиан OA=2OE,OB=2OD и OC=2OF, тогда при гомотетии с центром в точке O и k=-1/2, треугольник ABC>треугольник DEF, значит окружность, описанная около треугольник ABC, переходит в окружность, описанную около треугольник DEF, а R=2r,что и требовалось доказать.
Похожие решебники
Популярные решебники 9 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением