Упр.1358 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 9 класс, Просвещение:
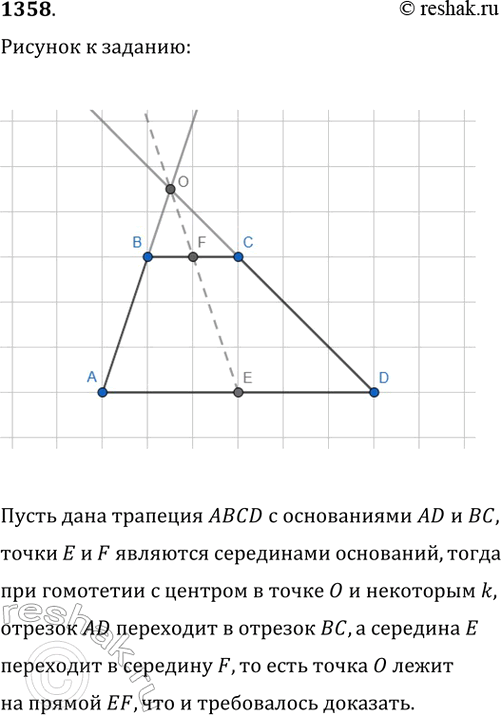
1358. Пусть точка О — точка пересечения прямых, содержащих боковые стороны данной трапеции. Используя гомотетию с центром в точке О, докажите, что точка О лежит на прямой, проходящей через середины оснований трапеции.
Пусть дана трапеция ABCD с основаниями AD и BC, точки E и F являются серединами оснований, тогда при гомотетии с центром в точке O и некоторым k, отрезок AD переходит в отрезок BC, а середина E переходит в середину F, то есть точка O лежит на прямой EF, что и требовалось доказать.
Похожие решебники
Популярные решебники 9 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







