Упр.1356 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 9 класс, Просвещение:
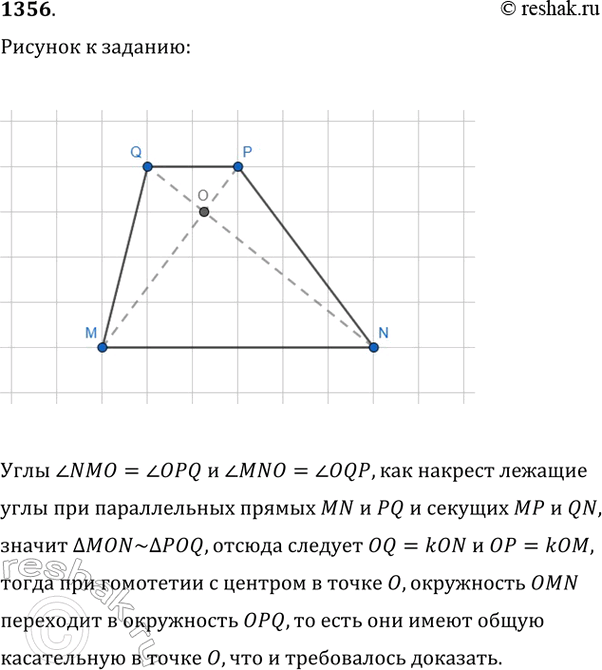
1356. В трапеции с основаниями MN и PQ диагонали МР и NQ пересекаются в точке О. Используя предыдущую задачу, докажите, что окружности, описанные около треугольников MNO и PQO, имеют общую касательную в точке О.
Углы угол NMO=угол OPQ и угол MNO=угол OQP,как накрест лежащие углы при параллельных прямых MN и PQ и секущих MP и QN, значит треугольник MON~треугольник POQ,отсюда следует OQ=kON и OP=kOM, тогда при гомотетии с центром в точке O, окружность OMN переходит в окружность OPQ, то есть они имеют общую касательную в точке O, что и требовалось доказать.
Похожие решебники
Популярные решебники 9 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







