Упр.6.75 ГДЗ Погорелов 7-9 класс (Геометрия)
Решение #1
Рассмотрим вариант решения задания из учебника Погорелов 8 класс, Просвещение:
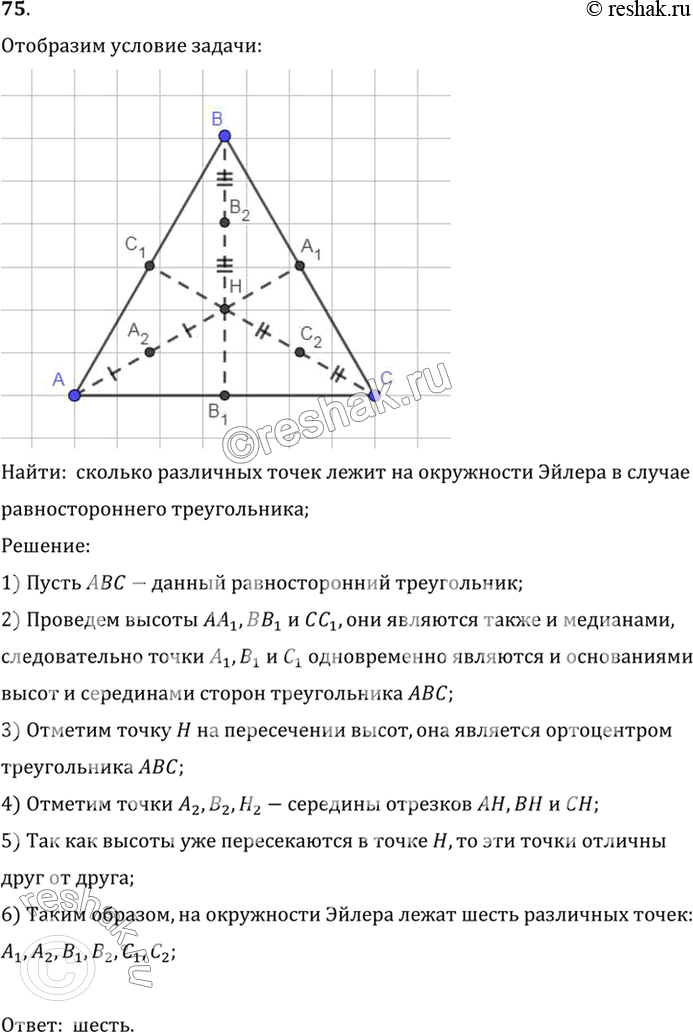
75. В общем случае на окружности Эйлера лежат девять точек (середины сторон треугольника, середины отрезков, соединяющих его ортоцентр с вершинами, и основания высот треугольника). Сколько различных точек из них лежит на окружности Эйлера в случае равностороннего треугольника?
Найти: сколько различных точек лежит на окружности Эйлера в случае
равностороннего треугольника;
Решение:
1) Пусть ABC-данный равносторонний треугольник;
2) Проведем высоты AA1, BB1 и CC1, они являются также и медианами,
следовательно точки A1, B1 и C1 одновременно являются и основаниями
высот и серединами сторон треугольника ABC;
3) Отметим точку H на пересечении высот, она является ортоцентром
треугольника ABC;
4) Отметим точки A2, B2, H2-середины отрезков AH, BH и CH;
5) Так как высоты уже пересекаются в точке H, то эти точки отличны
друг от друга;
6) Таким образом, на окружности Эйлера лежат шесть различных точек:
A1, A2, B1, B2, C1, C2;
Ответ: шесть.
Популярные решебники 8 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением