Упр.542 ГДЗ Мерзляк Полонский 5 класс (Математика)
Решение #1 (Учебник 2024)
Решение #2 (Учебник 2024)
Решение #3 (Учебник 2019)
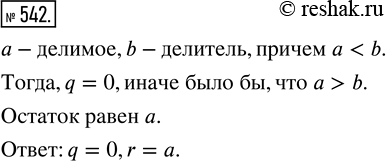
Решение #4 (Учебник 2019)
Рассмотрим вариант решения задания из учебника Мерзляк, Полонский, Якир 5 класс, Просвещение:
Фермер привёз на рынок 420 кг яблок и 180 кг груш в 50 ящиках. Сколько ящиков было с яблоками и сколько — с грушами, если известно, что массы всех ящиков равны?
Составим краткую запись по условиям задачи.
Яблоки 420 кг, ? ящиков
Груши 180 кг, ? ящиков
Найдём массу фруктов, которая вмещается в один ящик.
Разделив массу фруктов на вместимость одного ящика, получим количество ящиков.
Вместимость одного ящика можно найти, разделив общую массу фруктов на общее количество ящиков (50).
420+180=600 (кг) – фруктов всего.
600:50=12 (кг) – фруктов вмещается в один ящик.
Делим массу яблок (420 кг) на вместимость одного ящика (12 кг).
420:12=35 (ящ.) – с яблоками.
Делим массу груш (180 кг) на вместимость одного ящика (12 кг).
180:12=15 (ящ.) – с грушами.
Ответ: 35 ящиков с яблоками и 15 ящиков с грушами.
Известно, что число а — делимое, число b — делитель, причём а < b. Найдите неполное частное и остаток при делении числа а на число b.
Для того, чтобы найти делимое, необходимо делитель умножить на неполное частное и прибавить остаток.
В буквенном виде это правило можно записать так:
a=bq+r, где a – делимое, b – делитель, q – неполное частное, r – остаток, r<b.
По условию a<b, значит, чтобы равенство a=bq+r было справедливо, неполное частное должно равняться нулю.
Тогда, a=b•0+r и a=r.
То есть получили, что неполное частное равно 0, остаток - a.
Похожие решебники
Популярные решебники 5 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением