Упр.5.88 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
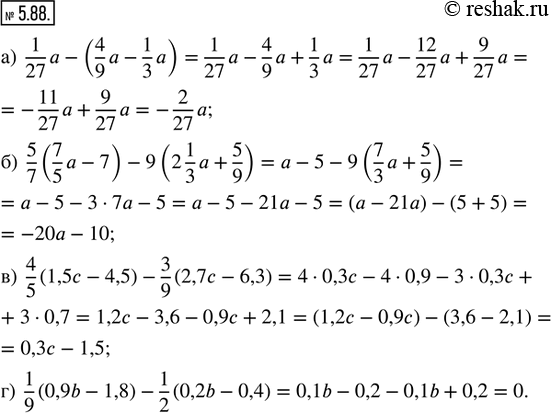
Решение #2 (Учебник 2023)


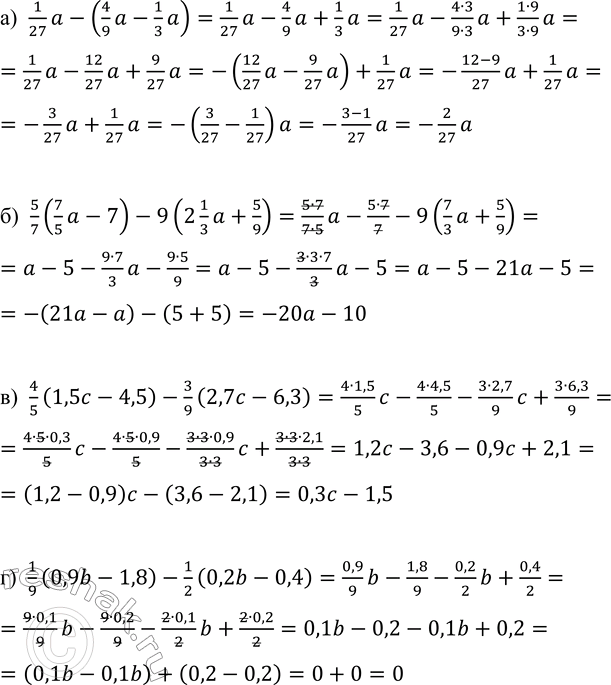
Решение #3 (Учебник 2023)
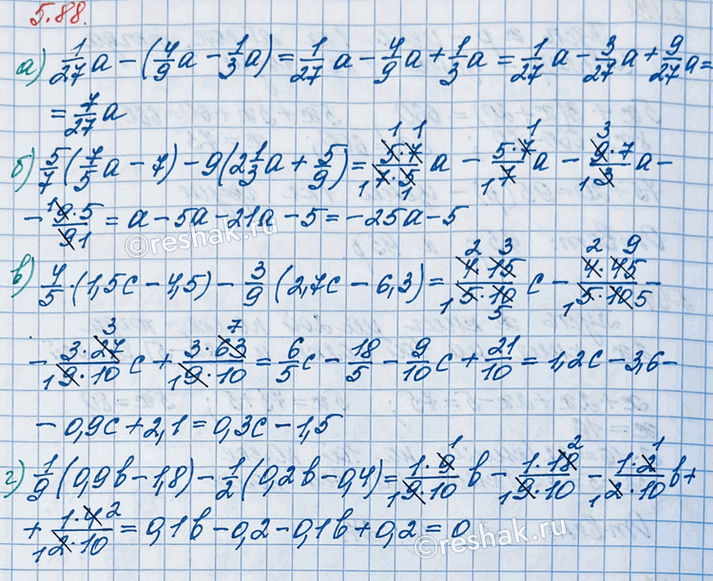
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Упростите выражение:
а) 1/27 a - (4/9 a - 1/3 a); в) 4/5 (1,5c - 4,5) - 3/9 (2,7c - 6,3);
б) 5/7 (7/5 a - 7) - 9(2 1/3 a + 5/9); г) 1/9 (0,9b - 1,8) - 1/2 (0,2b - 0,4).
Сначала раскроем скобки. Для этого необходимо множитель, стоящий за скобками, умножить на каждое слагаемое, стоящее в скобках, затем приводим подобные слагаемые.
Для того, чтобы сложить (привести) подобные слагаемые, необходимо сложить их коэффициенты и полученный результат умножить на общую буквенную часть.
При выполнении вычислений опираемся на следующие правила:
- для того, чтобы перемножить два числа с разными знаками, необходимо умножить их модули и перед полученным произведением поставить знак «-».
- для того, чтобы перемножить два отрицательных числа, необходимо перемножить их модули.
- для того, чтобы сложить два числа с разными знаками, необходимо найти модули слагаемых и из большего модуля вычесть меньший модуль; перед полученным числом поставить знак слагаемого с большим модулем.
- для того, чтобы сложить два отрицательных числа, необходимо найти и сложить модули слагаемых; перед полученным числом поставить знак «-».
- для того, чтобы из данного числа вычесть другое, необходимо к уменьшаемому прибавить число, противоположное вычитаемому.
- для того, чтобы найти сумму (разность) двух дробей с одинаковыми знаменателями, необходимо сложить (вычесть) их числители, а знаменатель оставить прежним.
- для того, чтобы сложить (вычесть) две дроби с разными знаменателями, необходимо привести данные дроби к общему знаменателю и применить правило сложения (вычитания) дробей с одинаковыми знаменателями, то есть сложить (вычесть) числители, а знаменатель оставить прежним.
- для того, чтобы умножить обыкновенную дробь на натуральное число (десятичную дробь), необходимо её числитель умножить на это число, а знаменатель оставить без изменения.
- для того, чтобы выполнить умножение смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части, эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
Также при выполнении умножения обыкновенных дробей, если возможно, выполняем сокращение.
а) 1/27 a-(4/9 a-1/3 a)=1/27 a-4/9 a+1/3 a=1/27 a-(4•3)/(9•3) a+(1•9)/(3•9) a=1/27 a-12/27 a+9/27 a=-(12/27 a-9/27 a)+1/27 a=-(12-9)/27 a+1/27 a=-3/27 a+1/27 a=-(3/27-1/27)a=-(3-1)/27 a=-2/27 a
б) 5/7 (7/5 a-7)-9(2 1/3 a+5/9)=(5•7)/(7•5) a-(5•7)/7-9(7/3 a+5/9)=a-5-(9•7)/3 a-(9•5)/9=a-5-(3•3•7)/3 a-5=a-5-21a-5=-(21a-a)-(5+5)=-20a-10
в) 4/5 (1,5c-4,5)-3/9 (2,7c-6,3)=(4•1,5)/5 c-(4•4,5)/5-(3•2,7)/9 c+(3•6,3)/9=(4•5•0,3)/5 c-(4•5•0,9)/5-(3•3•0,9)/(3•3) c+(3•3•2,1)/(3•3)=1,2c-3,6-0,9c+2,1=(1,2-0,9)c-(3,6-2,1)=0,3c-1,5
г) 1/9 (0,9b-1,8)-1/2 (0,2b-0,4)=0,9/9 b-1,8/9-0,2/2 b+0,4/2=(9•0,1)/9 b-(9•0,2)/9-(2•0,1)/2 b+(2•0,2)/2=0,1b-0,2-0,1b+0,2=(0,1b-0,1b)+(0,2-0,2)=0+0=0
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.