Упр.5.12 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1(Учебник 2026)
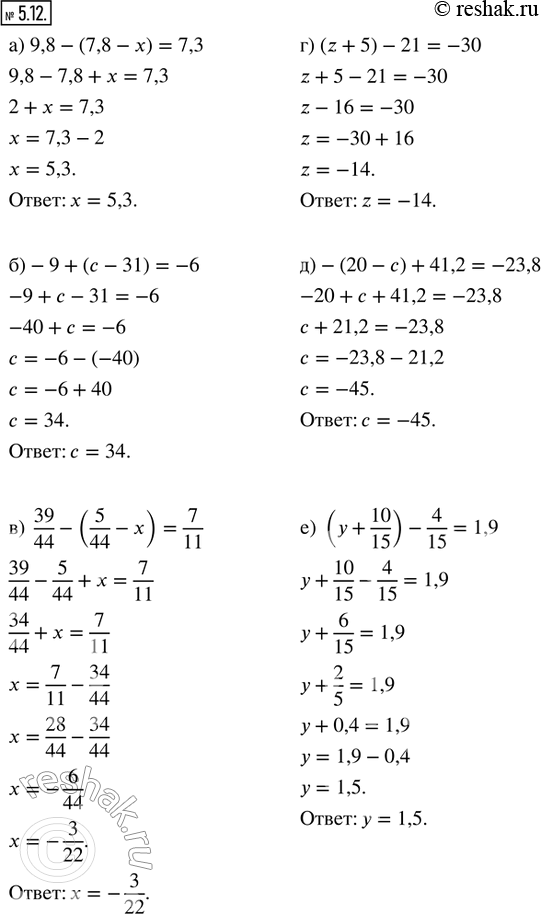
Решение #2(Учебник 2026)
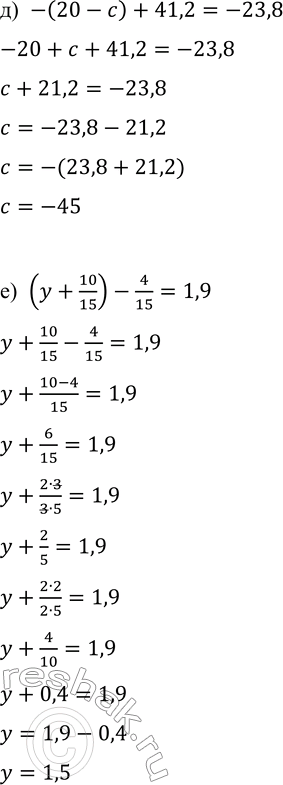
Решение #3(Учебник 2026)
Решение #4 (Учебник 2026)ИИ
Раскрыть скобки и решить уравнения
С пояснением а) 9,8 − (7,8 − x) = 7,3.
9,8 − 7,8 + x = 7,3.
2 + x = 7,3.
x = 7,3 − 2.
x = 5,3.
б) −9 + (c − 31) = −6.
−9 + c − 31 = −6.
c − 40 = −6.
c = −6 + 40.
c = 34.
в) 39/44 − (5/44 − x) = 7/11.
39/44 − 5/44 + x = 7/11.
34/44 + x = 28/44.
x = 28/44 − 34/44.
x = −6/44 = −3/22.
г) (z + 5) − 21 = −30.
z + 5 − 21 = −30.
z − 16 = −30.
z = −30 + 16.
z = −14.
д) −(20 − c) + 41,2 = −23,8.
−20 + c + 41,2 = −23,8.
c + 21,2 = −23,8.
c = −23,8 − 21,2.
c = −45.
е) (y + 10/15) − 4/15 = 1,9.
y + 6/15 = 1,9.
y + 0,4 = 1,9.
y = 1,9 − 0,4.
y = 1,5.
Ответ: а) x = 5,3; б) c = 34; в) x = −3/22; г) z = −14; д) c = −45; е) y = 1,5.
Кратко а) 9,8 − 7,8 + x = 7,3;
x = 5,3.
б) c − 40 = −6;
c = 34.
в) 34/44 + x = 28/44;
x = −3/22.
г) z − 16 = −30;
z = −14.
д) c + 21,2 = −23,8;
c = −45.
е) y + 0,4 = 1,9;
y = 1,5.
Ответ: а) x = 5,3; б) c = 34; в) x = −3/22; г) z = −14; д) c = −45; е) y = 1,5.
С пояснением а) 9,8 − (7,8 − x) = 7,3.
9,8 − 7,8 + x = 7,3.
2 + x = 7,3.
x = 7,3 − 2.
x = 5,3.
б) −9 + (c − 31) = −6.
−9 + c − 31 = −6.
c − 40 = −6.
c = −6 + 40.
c = 34.
в) 39/44 − (5/44 − x) = 7/11.
39/44 − 5/44 + x = 7/11.
34/44 + x = 28/44.
x = 28/44 − 34/44.
x = −6/44 = −3/22.
г) (z + 5) − 21 = −30.
z + 5 − 21 = −30.
z − 16 = −30.
z = −30 + 16.
z = −14.
д) −(20 − c) + 41,2 = −23,8.
−20 + c + 41,2 = −23,8.
c + 21,2 = −23,8.
c = −23,8 − 21,2.
c = −45.
е) (y + 10/15) − 4/15 = 1,9.
y + 6/15 = 1,9.
y + 0,4 = 1,9.
y = 1,9 − 0,4.
y = 1,5.
Ответ: а) x = 5,3; б) c = 34; в) x = −3/22; г) z = −14; д) c = −45; е) y = 1,5.
Кратко а) 9,8 − 7,8 + x = 7,3;
x = 5,3.
б) c − 40 = −6;
c = 34.
в) 34/44 + x = 28/44;
x = −3/22.
г) z − 16 = −30;
z = −14.
д) c + 21,2 = −23,8;
c = −45.
е) y + 0,4 = 1,9;
y = 1,5.
Ответ: а) x = 5,3; б) c = 34; в) x = −3/22; г) z = −14; д) c = −45; е) y = 1,5.
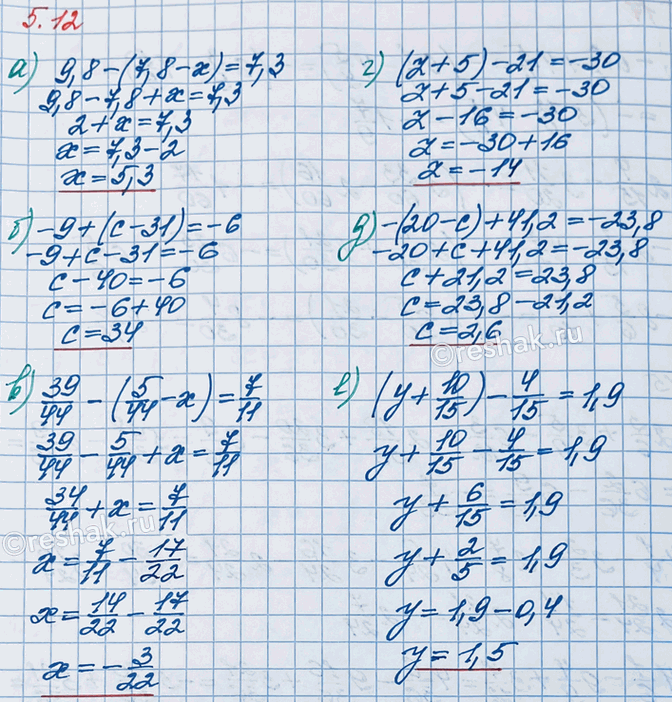
Рассмотрим вариант решения задания из учебника
Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Задание учебника 2026 года
Раскройте скобки и решите уравнение:
а) 9,8 - (7,8 - x ) = 7,3; г) (z + 5) -21 = -30;
б) -9 + (c - 31) = -6; д) -(20 - c) + 41,2 = -23,8;
в) 39/44 - (5/44 - x) = 7/11; е) (y + 10/15) - 4/15 = 1,9.
Уравнение – это равенство, содержащее букву, значение которой необходимо найти.
Корень уравнения – это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.
Решить уравнение – значит найти все его корни или показать, что их нет вообще.
При решении уравнений помним, что:
- для того, чтобы найти неизвестное слагаемое, необходимо из суммы вычесть известное слагаемое.
- для того, чтобы найти неизвестное уменьшаемое, необходимо к разности прибавить вычитаемое.
- для того, чтобы найти неизвестное вычитаемое, необходимо из уменьшаемого вычесть разность.
Если перед скобками стоит знак «+», то можно опустить скобки и этот знак «+», сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его необходимо записать со знаком «+».
Для того, чтобы раскрыть скобки, перед которыми стоит знак «-», необходимо заменить этот знак на «-», поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.
Для того, чтобы найти сумму (разность) двух дробей с одинаковыми знаменателями, необходимо сложить (вычесть) их числители, а знаменатель оставить прежним.
Для того, чтобы сложить (вычесть) две дроби с разными знаменателями, необходимо привести данные дроби к общему знаменателю и применить правило сложения (вычитания) дробей с одинаковыми знаменателями.
Для того, чтобы из данного числа вычесть другое, необходимо к уменьшаемому прибавить число, противоположное вычитаемому.
Для того, чтобы сложить два числа с разными знаками, необходимо найти модули слагаемых и из большего модуля вычесть меньший модуль; перед полученным числом поставить знак слагаемого с большим модулем.
Для того, чтобы сложить два отрицательных числа, необходимо найти и сложить модули слагаемых; перед полученным числом поставить знак «-».
а) 9,8-(7,8-x)=7,3
9,8-7,8+x=7,3
2+x=7,3
x=7,3-2
x=5,3
б) -9+(c-31)=-6
-9+c-31=-6
c-(9+31)=-6
c-40=-6
c=-6+40
c=40-6
c=34
в) 39/44-(5/44-x)=7/11
39/44-5/44+x=7/11
(39-5)/44+x=7/11
34/44+x=7/11
x=7/11-34/44
x=(7•2)/(11•2)-(17•2)/(22•2)
x=14/22-17/22
x=-(17/22-14/22)
x=-(17-14)/22
x=-3/22
г) (z+5)-21=-30
z+5-21=-30
z-(21-5)=-30
z-16=-30
z=-30+16
z=-(30-16)
z=-14
д) -(20-c)+41,2=-23,8
-20+c+41,2=-23,8
c+21,2=-23,8
c=-23,8-21,2
c=-(23,8+21,2)
c=-45
е) (y+10/15)-4/15=1,9
y+10/15-4/15=1,9
y+(10-4)/15=1,9
y+6/15=1,9
y+(2•3)/(3•5)=1,9
y+2/5=1,9
y+(2•2)/(2•5)=1,9
y+4/10=1,9
y+0,4=1,9
y=1,9-0,4
y=1,5
