Упр.4.310 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
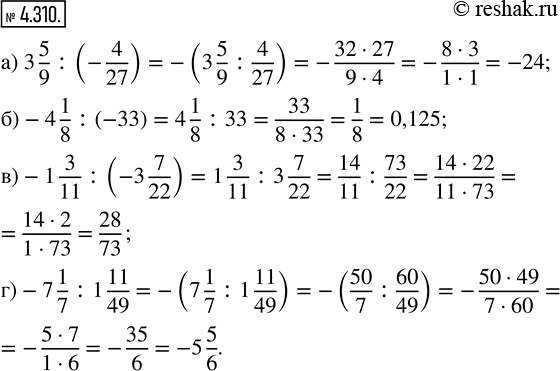
Решение #2 (Учебник 2023)
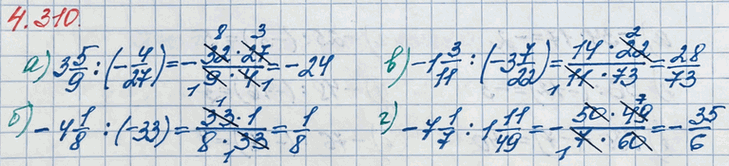
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Выполните деление:
а) 3 5/9 : (-4/27); б) -4 1/8 : (-33); в) -1 3/11 : (-3 7/22); г) -7 1/7 : 1 11/49.
При выполнении деления опираемся на следующие правила:
- для того, чтобы найти частное двух отрицательных чисел, необходимо разделить модуль делимого на модуль делителя.
- для того, чтобы найти частное двух чисел с разными знаками, необходимо разделить модуль делимого на модуль делителя и поставить перед полученным числом знак «-».
- для того, чтобы разделить одну дробь на другую, необходимо делимое умножить на число, обратное делителю, то есть у делителя нужно поменять местами числа, стоящие в числителе и знаменателе.
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
- для того, чтобы выполнить деление смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом деления дробей.
- для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
Если при вычислениях получаем неправильную дробь (числитель больше знаменателя), которую нельзя представить в виде десятичной дроби, то преобразуем её в смешанное число.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель его дробной части.
При вычислениях, если возможно, выполняем сокращение обыкновенных дробей.
а) 3 5/9 :(-4/27)=-(3 5/9 :4/27)=-(32/9 :4/27)=-(32/9•27/4)=-(32•27)/(9•4)==-(4•8•3•9)/(9•4)=-24/1=-24
б) -4 1/8 :(-33)=4 1/8 :33=33/8 :33/1=33/8•1/33=33/(8•33)=(1•125)/(8•125)=125/1000=0,125
в) -1 3/11 :(-3 7/22)=1 3/11 :3 7/22=14/11 :73/22=14/11•22/73=(14•22)/(11•73)=(14•2•11)/(11•73)=28/73
г) -7 1/7 :1 11/49=-(7 1/7 :1 11/49)=-(50/7 :60/49)=-(50/7•49/60)=-(50•49)/(7•60)=-(5•10•7•7)/(7•6•10)=-35/6=-5 5/6
Похожие решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением