Упр.4.304 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1
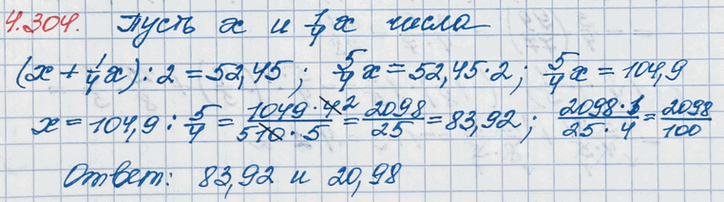
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
4.304. Одно из чисел составляет четверть другого. Найдите каждое число, если среднее арифметическое этих чисел равно 52,45.
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
