Упр.2.408 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
Решение #2 (Учебник 2023)
Решение #3 (Учебник 2023)
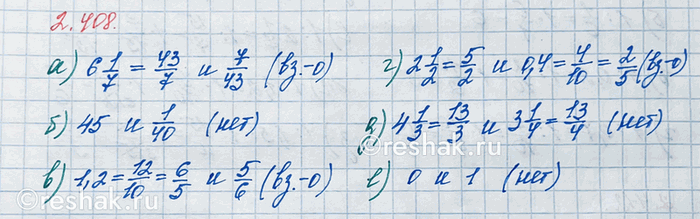
Решение #4 (Учебник 2021)
Решение #5 (Учебник 2021)
Решение #6 (Учебник 2021)
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Являются ли числа взаимно обратными:
а) 6 1/7 и 7/43; в) 1,2 и 5/6; д) 4 1/3 и 3 1/4;
6) 45 и 1/40; г) 2 1/2 и 0,4; е) 0 и 1?
Два числа, произведение которых равно 1, называют взаимно обратными.
Следовательно, чтобы проверить, будут ли представленные пары чисел взаимно обратными, необходимо их перемножить, если получим в произведении единицу, то числа будут взаимно обратными, если другое число, то не будут.
При выполнении умножения опираемся на следующие правила:
- чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменения.
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
- чтобы выполнить умножение смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
- для того, чтобы записать смешанное число в виде неправильной дроби, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
- при умножении обыкновенных дробей и смешанных чисел выполняем сокращение.
а) 6 1/7•7/43=43/7•7/43=(43•7)/(7•43)=1/1=1
6 1/7 и 7/43 - взаимно обратные числа.
б) 45•1/40=(45•1)/40=(5•9)/(5•8)=9/8=1 1/8 не равно 1
45 и 1/40 - не являются взаимно обратными числами.
в) 1,2•5/6=1 2/10•5/6=12/10•5/6=(2•6)/(2•5)•5/6=6/5•5/6=(6•5)/(5•6)=1/1=1
1,2 и 5/6 - взаимно обратные числа.
г) 2 1/2•0,4=2 1/2•4/10=2 1/2•(2•2)/(2•5)=5/2•2/5=(5•2)/(2•5)=1/1=1
2 1/2 и 0,4 - взаимно обратные числа.
д) 4 1/3•3 1/4=13/3•13/4=(13•13)/(3•4)=169/12=14 1/12 не равно 1
4 1/3 и 3 1/4 - не являются взаимно обратными числами.
е) 0•1=0 не равно 1
0 и 1 – не являются взаимно обратными числами.
а) Было собрано 180 кг яблок. На приготовление сока израсходовали 7/12 всех яблок, а остальные яблоки оставили в свежем виде на зиму. Сколько килограммов яблок было оставлено на зиму?
Для того, чтобы найти дробь от числа, необходимо эту дробь умножить на данное число.
По условию было собрано 180 кг яблок.
Из них 7/12 израсходовали на приготовление сока, то есть на приготовление сока израсходовали
7/12•180=(7•180)/12=(7•12•15)/12=105/1=105 (кг) - яблок.
Оставшиеся после приготовления сока яблоки, оставили в свежем виде на зиму.
Для того, чтобы найти, сколько яблок осталось, необходимо из массы собранных яблок вычесть массу яблок, которые израсходовали на приготовление сока, то есть на зиму было оставлено
180-105=75 (кг) – яблок.
Ответ: 75 кг.
б) Смородина — очень полезная ягода, богатая витамином С. В саду посажены 24 куста чёрной и красной смородины. Красная смородина составила 0,25 всех кустов. Сколько кустов чёрной смородины было посажено в саду?
Для того, чтобы найти дробь от числа, необходимо эту дробь умножить на данное число.
По условию посажено 24 куста смородины.
Из них 0,25 составляют кусты красной смородины, то есть кустов красной смородины
0,25•24=6,00=6 (кустов) – красной смородины.
Оставшиеся кусты – чёрная смородина.
Для того, чтобы найти, сколько кустов чёрной смородины посажено в саду, необходимо из общего количества кустов, посаженных в саду, вычесть количество кустов красной смородины, то есть в саду посажено
24-6=18 (кустов) – чёрной смородины.
Ответ: 75 кг.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением