Упр.2.412 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
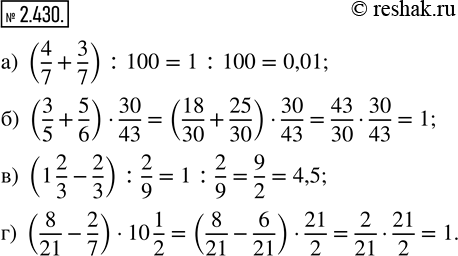
Решение #2 (Учебник 2023)
Решение #3 (Учебник 2023)
Решение #4 (Учебник 2021)
Решение #5 (Учебник 2021)
Решение #6 (Учебник 2021)
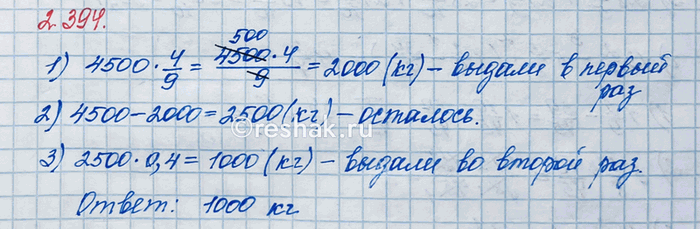
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Выполните действия:
а) (4/7 + 3/7) : 100; б) (3/5 + 5/6) · 30/43; в) (1 2/3 - 2/3) : 2/9; г) (8/21 - 2/7) · 10 1/2.
При умножении числителя и знаменателя дроби на одно и то же число, получается дробь равная данной.
При сложении (вычитании) дробей с одинаковыми знаменателями, их числители складывают, а знаменатель оставляют тот же.
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
Смешанные числа перед умножением необходимо представить в виде неправильных дробей.
Для того, чтобы записать смешанное число в виде неправильной дроби, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
а) (4/7+3/7) :100=(4+3)/7 :100=7/7 :100=1:100=0,01
б) (3/5+5/6)•30/43=((3•6)/(5•6)+(5•5)/(6•5))•30/43=(18/30+25/30)•30/43=43/30•30/43=(43•30)/(30•43)=1/1=1
в) (1 2/3-2/3) :2/9=1:2/9=9/2=4 1/2
г) (8/21-2/7)•10 1/2=(8/21-(2•3)/(7•3))•10 1/2=(8/21-6/21)•10 1/2=(8-6)/21•21/2=2/21•21/2=(2•21)/(21•2)=1/1=1
Со склада выдали в первый раз для штукатурки стен 4/9 имеющейся сухой смеси, а во второй раз — 0,4 оставшейся смеси. Сколько килограммов смеси выдали во второй раз, если на складе было 4500 кг?
Для того, чтобы найти дробь от числа, необходимо умножить дробь на данное число.
На складе было 4500 кг смеси для штукатурки стен.
В первый раз со склада выдали 4/9 имеющейся сухой смеси.
Поэтому, чтобы найти, сколько смеси выдали в первый раз, необходимо 4/9 умножить на массу смеси, которая была на складе первоначально, то есть в первый раз со склада выдали
4/9•4500=(4•4500)/9=(4•500•9)/9=2000/1=2000 (кг) – сухой смеси.
Для того, чтобы дробь умножить на натуральное число, необходимо умножить числитель дроби на это число, а знаменатель оставить без изменений.
Для того, чтобы найти, сколько смеси осталось после первой выдачи, необходимо из массы смеси, которая была на складе первоначально, вычесть массу смеси, которую выдали в первый раз, то есть на складе осталось
4500-2000=2500 (кг) - смеси.
По условию, во второй раз выдали 0,4 оставшейся смеси.
Для того, чтобы найти массу выданной смеси, необходимо 0,4 умножить на остаток смеси, получим, что во второй раз выдали
0,4•2500=1000,0=1000 (кг) – смеси.
Для того, чтобы умножить десятичную дробь на натуральное число, необходимо умножить их как натуральные числа, не обращая внимание на запятую; в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятой у умножаемой дроби.
Ответ: 1000 кг.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением