Упр.2.357 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
Решение #2 (Учебник 2023)
Решение #3 (Учебник 2023)
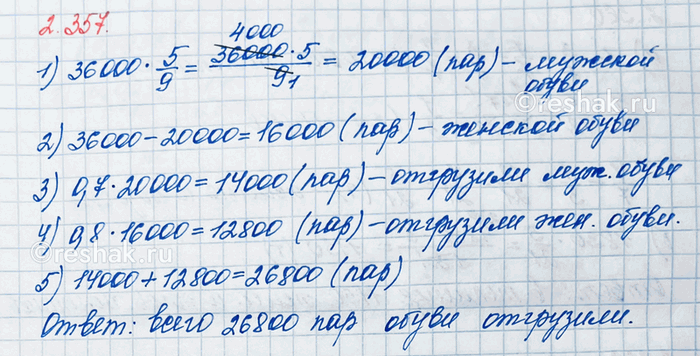
Решение #4 (Учебник 2021)
Решение #5 (Учебник 2021)
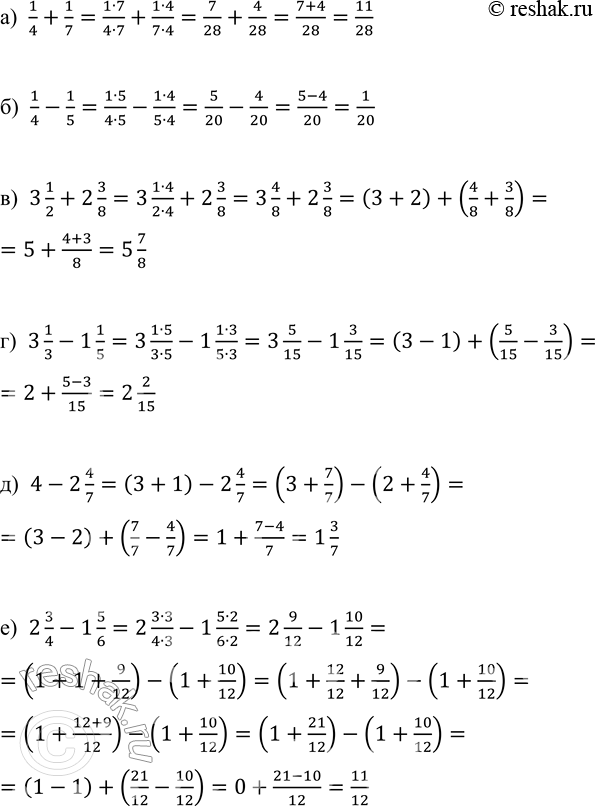
Решение #6 (Учебник 2021)
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Фабрика произвела 36 000 пар женской и мужской обуви. В магазины было отгружено 0,7 всех пар мужской обуви и 0,8 всех пар женской. Сколько пар обуви отгрузили в магазины, если мужская обувь составляет 5/9 всей обуви?
Фабрика произвела 36 000 пар обуви – женской и мужской.
Мужская обувь составляет 5/9 всей обуви.
Для того, чтобы найти дробь от числа, необходимо число умножить на эту дробь.
Значит, всего было произведено
36 000•5/9=(36000•5)/9=(9•4000•5)/9=(20 000)/1=20 000 (шт) – пар мужской обуви.
Для того, чтобы умножить обыкновенную дробь на натуральное число, необходимо её числитель умножить на это число, а знаменатель оставить без изменений.
Прежде, чем выполнить умножение, выполняем сокращение дробей (если это возможно), то есть делим числитель и знаменатель на одно и то же число (наибольший общий делитель).
Дробь, у которой в знаменателе стоит единица, равна числителю.
Соответственно, фабрика произвела
36 000-20 000=16 000 (шт) – пар женской обуви.
Для того, чтобы определить сколько пар мужской и женской обуви отгружено в магазины, необходимо количество произведённых пар умножить на долю отгруженных пар соответственно.
20 000•0,7=14 000 (шт) – пар мужской обуви было отгружено в магазины.
16 000•0,8=12 800 (шт) – пар женской обуви было отгружено в магазины.
Для того, чтобы умножить десятичную дробь на натуральное число, необходимо умножить их как натуральные числа, не обращая внимание на запятую; в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятой у умножаемой дроби.
Всего в магазины было отгружено
14 000+12 800=26 800 (шт) – пар обуви фабрики.
Ответ: 26 800 пар обуви.
Выполните действия:
а) 1/4 + 1/7; в) 3 1/2 + 2 3/8; д) 4 - 2 4/7;
б) 1/4 - 1/5; г) 3 1/3 - 1 1/5; е) 2 3/4 - 1 5/6.
При выполнении вычислений опираемся на следующие правила:
- для того, чтобы сложить дроби с разными знаменателями, необходимо сначала привести эти дроби к наименьшему общему знаменателю (используя дополнительные множители), а затем сложить их числители, а знаменатель оставить прежним.
- для того, чтобы вычесть дроби с разными знаменателями, необходимо сначала привести эти дроби к общему знаменателю (используя дополнительные множители), а затем из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
- для того, чтобы сложить смешанные числа, необходимо привести дробные части этих чисел к наименьшему общему знаменателю; отдельно выполнить сложение целых частей и отдельно дробных частей.
- для того, чтобы выполнить вычитание смешанных чисел, необходимо привести дробные части этих чисел к наименьшему общему знаменателю; если в уменьшаемом нет дробной части, то надо одну единицу целой части превратить в неправильную дробь с тем же знаменателем, что и у вычитаемого; далее отдельно выполнить вычитание целых частей и отдельно дробных частей.
а) 1/4+1/7=(1•7)/(4•7)+(1•4)/(7•4)=7/28+4/28=(7+4)/28=11/28
б) 1/4-1/5=(1•5)/(4•5)-(1•4)/(5•4)=5/20-4/20=(5-4)/20=1/20
в) 3 1/2+2 3/8=3 (1•4)/(2•4)+2 3/8=3 4/8+2 3/8=(3+2)+(4/8+3/8)=5+(4+3)/8=5 7/8
г) 3 1/3-1 1/5=3 (1•5)/(3•5)-1 (1•3)/(5•3)=3 5/15-1 3/15=(3-1)+(5/15-3/15)=2+(5-3)/15=2 2/15
д) 4-2 4/7=(3+1)-2 4/7=(3+7/7)-(2+4/7)=(3-2)+(7/7-4/7)=1+(7-4)/7=1 3/7
е) 2 3/4-1 5/6=2 (3•3)/(4•3)-1 (5•2)/(6•2)=2 9/12-1 10/12=(1+1+9/12)-(1+10/12)=(1+12/12+9/12)-(1+10/12)=(1+(12+9)/12)-(1+10/12)=(1+21/12)-(1+10/12)=(1-1)+(21/12-10/12)=0+(21-10)/12=11/12
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением