Упр.73 ГДЗ Колягин Ткачёва 8 класс (Алгебра)
Решение #1 (Учебник 2024)
Решение #2 (Учебник 2013)
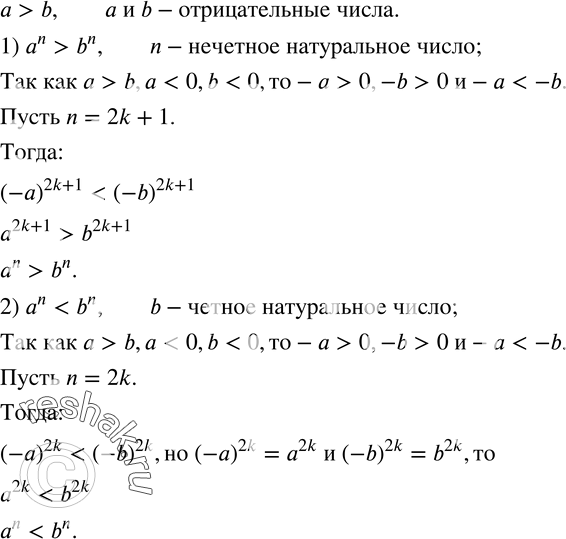
Рассмотрим вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 8 класс, Просвещение:
Выполнить действия:
1) (a^2+ab)/(a^2+b^2 ) · (a/(a-b) - a/(a+b));
2) (ab-b^2)/(a^2+b^2 ) · (a/(a+b) + b/(a-b));
3) ((c+d)/c - 2c/(c-d)) · (d-c)/(c^2+d^2 );
4) (2c/(c+d) + (d-c)/c) · (c+d)/(c^2+d^2 ).
Пусть a>b и числа a, b отрицательные. Доказать, что:
1) a^n>b^n, если n-нечетное натуральное число;
2) a^n<b^n, если b-четное натуральное число.
Популярные решебники 8 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.