Упр.4.279 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
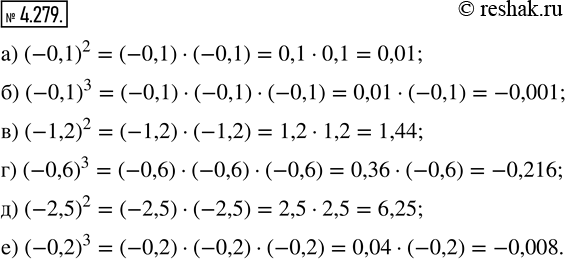
Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)
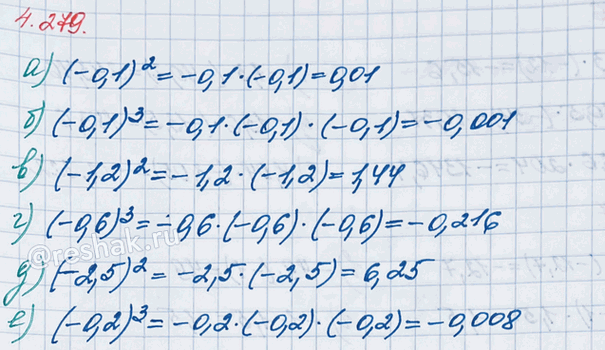
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Вычислите степень числа:
а) (-0,1)^2; б) (-0,1)^3; в) (-1,2)^2; г) (-0,6)^3; д) (-2,5)^2; е) (-0,2)^3.
Для того, чтобы число возвести в степень, необходимо умножить это число само на себя столько раз, какова его степень.
При выполнении вычислений опираемся на следующие правила:
- для того, чтобы перемножить два числа с разными знаками, необходимо умножить их модули и перед полученным произведением поставить знак «-».
- для того, чтобы перемножить два отрицательных числа, необходимо перемножить их модули.
- для того, чтобы перемножить две десятичные дроби, необходимо умножить их как натуральные числа, не обращая внимание на запятые; в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
а) (-0,1)^2=-0,1•(-0,1)=0,1•0,1=0,01
б) (-0,1)^3=-0,1•(-0,1)•(-0,1)=0,1•0,1•(-0,1)=0,01•(-0,1)=-(0,01•0,1)=-0,001
в) (-1,2)^2=-1,2•(-1,2)=1,2•1,2=1,44
г) (-0,6)^3=-0,6•(-0,6)•(-0,6)=0,6•0,6•(-0,6)=0,36•(-0,6)=-(0,36•0,6)=-0,216
д) (-2,5)^2=-2,5•(-2,5)=2,5•2,5=6,25
е) (-0,2)^3=-0,2•(-0,2)•(-0,2)=0,2•0,2•(-0,2)=0,04•(-0,2)=-(0,04•0,2)=-0,008
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.