Упр.4.262 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1(Учебник 2026)
Решение #2(Учебник 2026)
Решение #3(Учебник 2026)
Решение #4 (Учебник 2026)ИИ
Варианты решения:
Определить число участников каждого класса
С пояснением Пусть x — число шестиклассников. Тогда семиклассников было 0,6x, а пятиклассников — 1,5(x + 0,6x).
Составим уравнение по общему числу участников:
x + 0,6x + 1,5(x + 0,6x) = 40;
1,6x + 2,4x = 40;
4x = 40;
x = 10.
Значит, шестиклассников было 10.
0,6 · 10 = 6 (учащихся) — семиклассники.
1,5 · (10 + 6) = 24 (учащихся) — пятиклассники.
Ответ: 24 пятиклассника, 10 шестиклассников, 6 семиклассников.
Кратко Пусть x — число шестиклассников. Тогда семиклассников — 0,6x, а пятиклассников — 1,5(x + 0,6x).
x + 0,6x + 1,5(x + 0,6x) = 40;
4x = 40;
x = 10.
0,6 · 10 = 6 (учащихся) — семиклассников;
1,5 · (10 + 6) = 24 (учащихся) — пятиклассников.
Ответ: 24 пятиклассника, 10 шестиклассников, 6 семиклассников.
С пояснением Пусть x — число шестиклассников. Тогда семиклассников было 0,6x, а пятиклассников — 1,5(x + 0,6x).
Составим уравнение по общему числу участников:
x + 0,6x + 1,5(x + 0,6x) = 40;
1,6x + 2,4x = 40;
4x = 40;
x = 10.
Значит, шестиклассников было 10.
0,6 · 10 = 6 (учащихся) — семиклассники.
1,5 · (10 + 6) = 24 (учащихся) — пятиклассники.
Ответ: 24 пятиклассника, 10 шестиклассников, 6 семиклассников.
Кратко Пусть x — число шестиклассников. Тогда семиклассников — 0,6x, а пятиклассников — 1,5(x + 0,6x).
x + 0,6x + 1,5(x + 0,6x) = 40;
4x = 40;
x = 10.
0,6 · 10 = 6 (учащихся) — семиклассников;
1,5 · (10 + 6) = 24 (учащихся) — пятиклассников.
Ответ: 24 пятиклассника, 10 шестиклассников, 6 семиклассников.
Определить число участников каждого класса
С пояснением 1) Примем число шестиклассников за 1 часть. Тогда семиклассников было 0,6 части, а вместе шестиклассников и семиклассников — 1 + 0,6 = 1,6 части.
2) Пятиклассников было в 1,5 раза больше: 1,6 · 1,5 = 2,4 части.
3) Всего частей: 1 + 0,6 + 2,4 = 4 (части).
4) 40 : 4 = 10 (учащихся) — шестиклассников.
5) 10 · 0,6 = 6 (учащихся) — семиклассников.
6) 10 + 6 = 16 (учащихся) — шестиклассников и семиклассников вместе; 16 · 1,5 = 24 (учащихся) — пятиклассников.
Ответ: 24 пятиклассника, 10 шестиклассников, 6 семиклассников.
Кратко 1) 1 + 0,6 = 1,6 (части) — шестиклассники и семиклассники вместе.
2) 1,6 · 1,5 = 2,4 (части) — пятиклассники.
3) 1 + 0,6 + 2,4 = 4 (части); 40 : 4 = 10 (учащихся) — шестиклассников.
4) 10 · 0,6 = 6 (учащихся) — семиклассников; 10 + 6 = 16, 16 · 1,5 = 24 (учащихся) — пятиклассников.
Ответ: 24 пятиклассника, 10 шестиклассников, 6 семиклассников.
С пояснением 1) Примем число шестиклассников за 1 часть. Тогда семиклассников было 0,6 части, а вместе шестиклассников и семиклассников — 1 + 0,6 = 1,6 части.
2) Пятиклассников было в 1,5 раза больше: 1,6 · 1,5 = 2,4 части.
3) Всего частей: 1 + 0,6 + 2,4 = 4 (части).
4) 40 : 4 = 10 (учащихся) — шестиклассников.
5) 10 · 0,6 = 6 (учащихся) — семиклассников.
6) 10 + 6 = 16 (учащихся) — шестиклассников и семиклассников вместе; 16 · 1,5 = 24 (учащихся) — пятиклассников.
Ответ: 24 пятиклассника, 10 шестиклассников, 6 семиклассников.
Кратко 1) 1 + 0,6 = 1,6 (части) — шестиклассники и семиклассники вместе.
2) 1,6 · 1,5 = 2,4 (части) — пятиклассники.
3) 1 + 0,6 + 2,4 = 4 (части); 40 : 4 = 10 (учащихся) — шестиклассников.
4) 10 · 0,6 = 6 (учащихся) — семиклассников; 10 + 6 = 16, 16 · 1,5 = 24 (учащихся) — пятиклассников.
Ответ: 24 пятиклассника, 10 шестиклассников, 6 семиклассников.
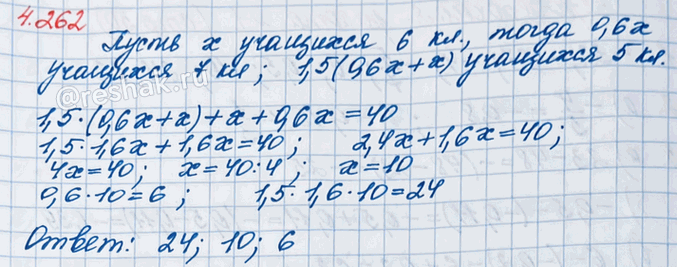
Рассмотрим вариант решения задания из учебника
Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Задание учебника 2026 года
В школьном конкурсе чтецов участвовало 40 человек. Учащихся 5 классов было в 1,5 раза больше, чем учащихся 6 и 7 классов вместе. Семиклассники составляли 0,6 от числа шестиклассников. Сколько учащихся каждого класса принимало участие в конкурсеугол Решим данную задачу с помощью уравнения.
Примем за неизвестную x число шестиклассников, участвовавших в конкурсе чтецов.
По условию семиклассники составляли 0,6 от числа шестиклассников, а чтобы найти дробь от числа, необходимо умножить число на эту дробь, значит, семиклассников было 0,6x
Значит, учащихся 6 и 7 классов вместе было x+0,6x=1,6x.
Учащихся 5 классов было в 1,5 раза больше, чем учащихся 6 и 7 классов вместе, то есть 1,5•1,6x=2,4x человек.
В школьном конкурсе чтецов участвовало 40 человек, поэтому можно записать уравнение:
2,4x+1,6x=40
Или, после упрощения, 4x=40
Неизвестным является множитель x.
Для того, чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель, получим
x=40:4
x=10
Значит, в конкурсе участвовало 10 шестиклассников .
Семиклассников было 0,6x=0,6•10=6 человек.
Тогда, пятиклассников участвовало 40-10-6=30-6=24 человека.
Ответ: 24 пятиклассника, 10 шестиклассников, 6 семиклассников.
