Упр.2.285 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)
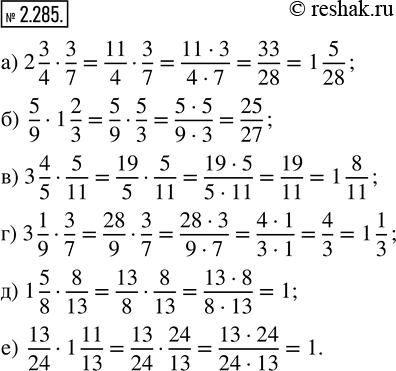
Решение #5 (Учебник 2021)

Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Двое друзей вышли навстречу друг другу и встретились в условленном месте. Какое расстояние было изначально между ними, если первый шёл 1 1/4 ч со скоростью 5 3/4 км/ч, а второй - 1 2/15 ч со скоростью 6 1/2 км/ч?
В примере даны смешанные числа, которые сначала необходимо представить в виде неправильных дробей, для этого нужно знаменатель умножить на целую часть и к полученному результату прибавить числитель, затем, то, что получили, записываем в числитель, знаменатель останется тот же.
Для того, чтобы умножить дробь на дробь, необходимо найти произведение числителей и знаменателей этих дробей. Первое произведение записать числителем, второе – знаменателем.
Составим схему задачи.
Найдём, какое расстояние прошёл каждый из друзей.
Для того, чтобы найти пройденное расстояние, необходимо скорость умножить на затраченное время.
5 3/4•1 1/4=23/4•5/4=(23•5)/(4•4)=115/16=7 3/16 (км) – прошёл первый друг.
6 1/2•1 2/15=13/2•17/15=(13•17)/(2•15)=221/30=7 11/30 (км) – прошёл второй друг.
Для того, чтобы найти изначальное расстояние между друзьями, необходимо сложить пройденные ими расстояния до места встречи.
7 3/16+7 11/30=7 (3•15)/(16•15)+7 (11•8)/(30•8)=7 45/240+7 88/240=(7+7)+(45/240+88/240)=14+(45+88)/240=14 133/240 (км) – изначальное расстояние между друзьями.
Ответ: 14 133/240 км.
Выполните действие:
а) 2 3/4 · 3/7; б) 5/9 · 1 2/3; в) 3 4/5 · 5/11; г) 3 1/9 · 3/7; д) 1 5/8 · 8/13; е) 13/24 · 1 11/13.
В примере даны смешанные числа, которые сначала необходимо представить в виде неправильных дробей, для этого нужно знаменатель умножить на целую часть и к полученному результату прибавить числитель, затем, то, что получили, записываем в числитель, знаменатель останется тот же.
Для того, чтобы умножить дробь на дробь, необходимо найти произведение числителей и знаменателей этих дробей. Первое произведение записать числителем, второе – знаменателем.
При умножении необходимо выполнять сокращение, если это возможно, для удобства расчётов. Для этого необходимо одно из чисел числителя и знаменателя разделить на одно и то же число и далее выполнять умножение.
а) 2 3/4•3/7=11/4•3/7=(11•3)/(4•7)=33/28=1 5/28
б) 5/9•1 2/3=5/9•5/3=(5•5)/(9•3)=25/27
в) 3 4/5•5/11=19/5•5/11=(19•5)/(5•11)=19/11=1 8/11
г) 3 1/9•3/7=28/9•3/7=(28•3)/(9•7)=(4•7•3)/(3•3•7)=4/3=1 1/3
д) 1 5/8•8/13=13/8•8/13=(13•8)/(8•13)=1/1=1
е) 13/24•1 11/13=13/24•24/13=(13•24)/(24•13)=1/1=1
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.