Упр.2.283 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)

Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)
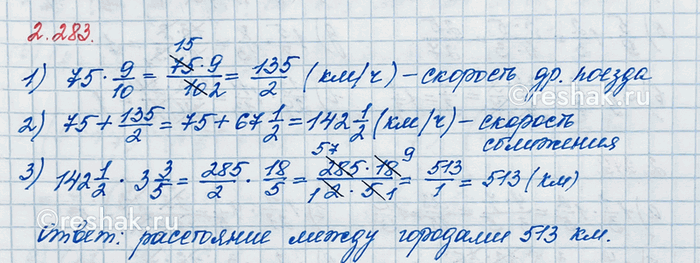
Решение #4 (Учебник 2021)
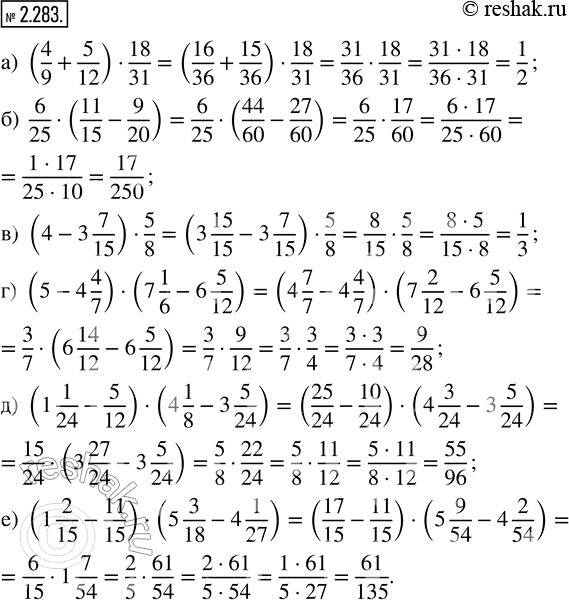
Решение #5 (Учебник 2021)

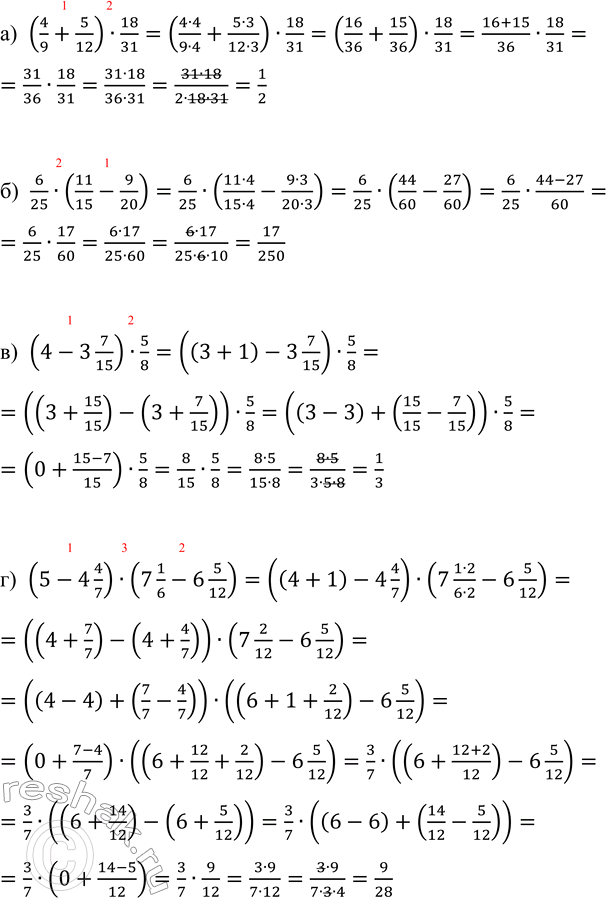
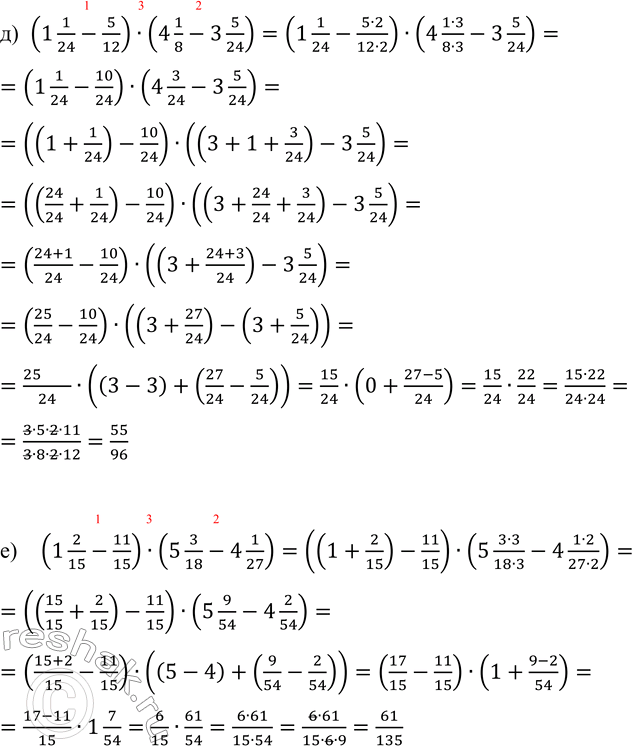
Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Из двух городов одновременно навстречу друг другу вышли два поезда и встретились через 3 3/5 ч. Найдите расстояние между городами, если скорость одного поезда равна 75 км/ч, а скорость другого составляет 9/10 от скорости первого поезда.
Для того, чтобы умножить дробь на дробь, необходимо найти произведение числителей и знаменателей этих дробей. Первое произведение записать числителем, второе – знаменателем.
Составим схему задачи.
Для начала найдём скорость второго поезда.
По условию, она составляет 9/10 от скорости первого поезда, тогда
75•9/10=(75•9)/10=(5•15•9)/(2•5)=135/2=67 1/2 (км/ч) – скорость второго поезда.
Поскольку, поезда выехали одновременно и движутся навстречу друг другу, то скорость их сближения равна сумме их скоростей.
Найдём скорость сближения поездов.
75+67 1/2=142 1/2 (км/ч) – скорость сближения поездов.
Для того, чтобы найти расстояние между городами из которых вышли поезда, необходимо скорость их сближения умножить на время в пути до их встречи.
142 1/2•3 3/5=285/2•18/5=(5•57•2•9)/(2•5)=513/1=513 (км) – расстояние между городами.
Ответ: 513 км.
Выполните действия:
а) (4/9 + 5/12) · 18/31; в) (4 - 3 7/15) · 5/8; д) (1 1/24 - 5/12) · (4 1/8 - 3 5/24);
б) 6/25 · (11/15 - 9/20); г) (5 - 4 4/7) · (7 1/6 - 6 5/12); е) (1 2/15 - 11/15) · (5 3/18 - 4 1/27).
Если в выражении есть скобки, то сначала выполняют действия в скобках.
Над примерами расставим цифрами порядок действий.
Для того, чтобы выполнить сложение смешанных чисел, необходимо дробные части привести к общему знаменателю, затем отдельно выполнить сложение целых частей и дробных частей.
При умножении числителя и знаменателя дроби на одно и то же число, получается дробь равная данной.
При сложении (вычитании) дробей с одинаковыми знаменателями, их числители складывают (вычитают), а знаменатель оставляют тот же.
Когда на первом месте стоит целое число и из него необходимо вычесть смешанное число, нужно целое число представить в виде смешанного числа, у которого дробная часть будет являться неправильной дробью.
Если при вычитании в первом числителе стоит число меньше, чем во втором числителе, то необходимо занять единицу у целой части и представить её в виде неправильной дроби совместно с данной дробью, затем отдельно выполнить вычитание целых частей и дробных частей.
Для того, чтобы умножить дробь на дробь, необходимо найти произведение числителей и знаменателей этих дробей. Первое произведение записать числителем, второе – знаменателем.
При умножении необходимо выполнять сокращение, если это возможно, для удобства расчётов. Для этого необходимо одно из чисел числителя и знаменателя разделить на одно и то же число и далее выполнять умножение.
а) (4/9+5/12)•18/31=((4•4)/(9•4)+(5•3)/(12•3))•18/31=(16/36+15/36)•18/31=(16+15)/36•18/31=31/36•18/31=(31•18)/(36•31)=(31•18)/(2•18•31)=1/2
б) 6/25•(11/15-9/20)=6/25•((11•4)/(15•4)-(9•3)/(20•3))=6/25•(44/60-27/60)=6/25•(44-27)/60=6/25•17/60=(6•17)/(25•60)=(6•17)/(25•6•10)=17/250
в) (4-3 7/15)•5/8=((3+1)-3 7/15)•5/8=((3+15/15)-(3+7/15))•5/8=((3-3)+(15/15-7/15))•5/8=(0+(15-7)/15)•5/8=8/15•5/8=(8•5)/(15•8)=(8•5)/(3•5•8)=1/3
г) (5-4 4/7)•(7 1/6-6 5/12)=((4+1)-4 4/7)•(7 (1•2)/(6•2)-6 5/12)=((4+7/7)-(4+4/7))•(7 2/12-6 5/12)=((4-4)+(7/7-4/7))•((6+1+2/12)-6 5/12)=(0+(7-4)/7)•((6+12/12+2/12)-6 5/12)=3/7•((6+(12+2)/12)-6 5/12)=3/7•((6+14/12)-(6+5/12))=3/7•((6-6)+(14/12-5/12))=3/7•(0+(14-5)/12)=3/7•9/12=(3•9)/(7•12)=(3•9)/(7•3•4)=9/28
д) (1 1/24-5/12)•(4 1/8-3 5/24)=(1 1/24-(5•2)/(12•2))•(4 (1•3)/(8•3)-3 5/24)=(1 1/24-10/24)•(4 3/24-3 5/24)= ((1+1/24)-10/24)•((3+1+3/24)-3 5/24)= ((24/24+1/24)-10/24)•((3+24/24+3/24)-3 5/24)=((24+1)/24-10/24)•((3+(24+3)/24)-3 5/24)=(25/24-10/24)•((3+27/24)-(3+5/24))=(25-10)/24•((3-3)+(27/24-5/24))=15/24•(0+(27-5)/24)=15/24•22/24=(15•22)/(24•24)==(3•5•2•11)/(3•8•2•12)=55/96
е) (1 2/15-11/15)•(5 3/18-4 1/27)=((1+2/15)-11/15)•(5 (3•3)/(18•3)-4 (1•2)/(27•2))=((15/15+2/15)-11/15)•(5 9/54-4 2/54)=((15+2)/15-11/15)•((5-4)+(9/54-2/54))=(17/15-11/15)•(1+(9-2)/54)=(17-11)/15•1 7/54=6/15•61/54=(6•61)/(15•54)=(6•61)/(15•6•9)=61/135
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.