Упр.2.233 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
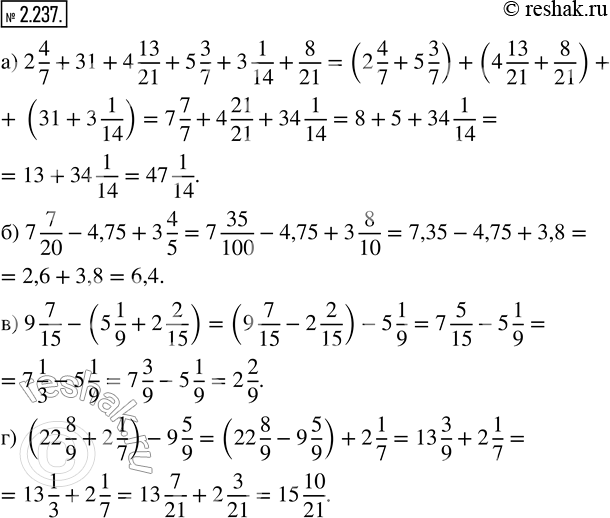
Решение #2 (Учебник 2023)
Решение #3 (Учебник 2023)
Решение #4 (Учебник 2021)
Решение #5 (Учебник 2021)
Решение #6 (Учебник 2021)
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Выполните действия:
а) 2 4/7 + 31 + 4 13/21 + 5 3/7 + 3 1/14 + 8/21; в) 9 7/15 - (5 1/9 + 2 2/15);
б) 7 7/20 - 4,75 + 3 4/5; г) (22 8/9 + 2 1/7) - 9 5/9.
Для того, чтобы выполнить сложение (вычитание) смешанных чисел, необходимо дробные части привести к общему знаменателю, затем отдельно выполнить сложение (вычитание) целых частей и дробных частей.
Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится дробь равная данной.
Если в ответе получается сократимая дробь, необходимо числитель и знаменатель разделить на одно и то же число.
а) Сгруппируем слагаемые дробные части которых содержат одинаковые знаменатели.
2 4/7+31+4 13/21+5 3/7+3 1/14+8/21=(2 4/7+5 3/7)+(4 13/21+8/21)+(31+3 1/14)=7 (4+3)/7+4 (13+8)/21+34 1/14=7 7/7+4 21/21+34 1/14=8+5+34 1/14=13+34 1/4=47 1/4
б) Переведём обыкновенные дроби в десятичные.
Для того, чтобы дробь 7 7/20 представить в виде десятичной дроби, сначала расширяем эту дробь на число 5 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 100.
7 7/20=7 (7•5)/(20•5)=7 35/100
Для того, чтобы получившуюся дробь записать в виде десятичной дроби, сначала пишем целую часть, а потом числитель дробной части (7,35).
Для того, чтобы дробь 3 4/5 представить в виде десятичной дроби, сначала расширяем эту дробь на число 2 (дополнительный множитель), чтобы в знаменателе получилась разрядная единица 10.
3 4/5=3 (4•2)/(5•2)=3 8/10
Для того, чтобы получившуюся дробь записать в виде десятичной дроби, сначала пишем целую часть, а потом числитель дробной части (3,8).
7 7/20-4,75+3 4/5=7,35-4,75+3,8=2,6+3,8=6,4
в) Для того, чтобы вычесть сумму 5 1/9+2 2/15 из дроби 9 7/15 , можно сначала вычесть из 9 7/15 слагаемое 2 2/15 с таким же знаменателем (15), и из полученной разности затем вычесть другое слагаемое 5 1/9 .
9 7/15-(5 1/9+2 2/15)=(9 7/15-2 2/15)-5 1/9=((9-2)+(7-2)/15)-5 1/9==7 5/15-5 1/9
Приведём дроби к общему знаменателю 45.
7 (5•3)/(15•3)-5 (1•5)/(9•5)=7 15/45-5 5/45=(7-5)+(15-5)/45
Сократим получившуюся дробь на 5.
2 10/45=2 (2•5)/(9•5)=2 2/9
г) Для того, чтобы вычесть дробь 9 5/9 из суммы 22 8/9+2 1/7 , можно 9 5/9 вычесть из 22 8/9 и полученную разность прибавить ко второму слагаемому 2 1/7 .
(22 8/9+2 1/7)-9 5/9=(22 8/9-9 5/9)+2 1/7=((22-9)+(8-5)/9)+2 1/7==13 3/9+2 1/7
Сократим первую дробь на 3.
13 3/9+2 1/7=13 (3•1)/(3•3)+2 1/7=13 1/3+2 1/7
Приведём дроби к общему знаменателю 21.
13 1/3+2 1/7=13 (1•7)/(3•7)+2 (1•3)/(7•3)=13 7/21+2 3/21=(13+2)+(7+3)/21=15 10/21
Скорость моторной лодки в стоячей воде равна 15 5/12 км/ч, а скорость течения реки - 2 3/4 км/ч. Найдите скорость моторной лодки по течению реки и против течения.
Для того, чтобы выполнить сложение (вычитание) смешанных чисел, необходимо дробные части привести к общему знаменателю, затем отдельно выполнить сложение (вычитание) целых частей и дробных частей.
При решении задач на движение по реке для того, чтобы найти скорость по течению, необходимо прибавить к собственной скорости скорость течения реки (река «подталкивает»), а для того, чтобы найти скорость против течения, необходимо вычесть из собственной скорости скорость течения реки (река «тормозит»).
Скорость лодки в стоячей воде равна 15 5/12 км/ч, - это собственная скорость моторной лодки.
Скорость течения реки - 2 3/4 км/ч.
Тогда, скорость моторной лодки по течению реки составит
15 5/12+2 3/4=15 5/12+2 (3•3)/(4•3)=15 5/12+2 9/12=15+2+(5+9)/12=17+14/12=17+1 2/12=18 (1•2)/(6•2)=18 1/6 (км/ч) – скорость лодки по течению реки.
Скорость моторной лодки против течения реки составит
15 5/12-2 3/4=15 5/12-2 (3•3)/(4•3)=15 5/12-2 9/12=(14+1+5/12)-2 9/12=(14+12/12+5/12)-2 9/12=(14+(12+5)/12)-2 9/12=14 17/12-2 9/12=(14-2)+(17/12-9/12)=12+(17-9)/12=12 8/12=12 (2•4)/(3•4)=12 2/3 (км/ч) – скорость лодки против течения реки.
Ответ: 18 1/6 км/ч,12 2/3 км/ч.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением