Упр.2.128 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
Решение #2 (Учебник 2023)
Решение #3 (Учебник 2023)
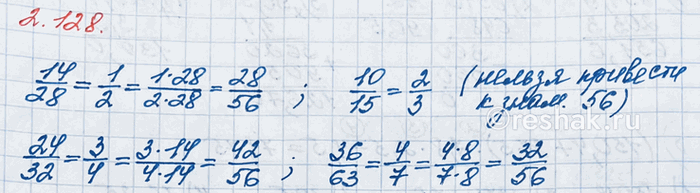
Решение #4 (Учебник 2021)
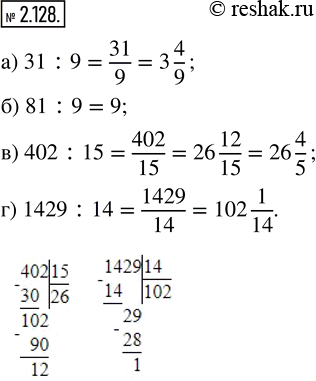
Решение #5 (Учебник 2021)
Решение #6 (Учебник 2021)
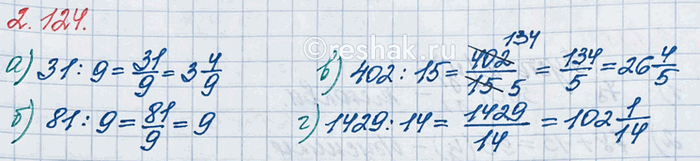
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Сократите дроби 14/28, 10/15, 24/32, 36/63 а затем приведите их к знаменателю 56.
14/28=(14•1)/(14•2)=1/2
После сокращения дроби 14/28 получили равную ей дробь 1/2 .
Для того, чтобы определить, на какое число необходимо умножить числитель и знаменатель дроби 1/2 (определить дополнительный множитель), чтобы знаменатель был равен 56, необходимо найти частное 56:2
56:2=28 - дополнительный множитель.
1/2=(1•28)/(2•28)=28/56
10/15=(2•5)/(3•5)=2/3
После сокращения дроби 10/15 получили равную ей дробь 2/3 .
Для того, чтобы определить, на какое число необходимо умножить числитель и знаменатель дроби 2/3 (определить дополнительный множитель), чтобы знаменатель был равен 56, необходимо найти частное 56:3
56:3=18 (ост.2)
Значит, данную дробь не получится привести к знаменателю 56.
24/32=(3•8)/(4•8)=3/4
После сокращения дроби 24/32 получили равную ей дробь 3/4 .
Для того, чтобы определить, на какое число необходимо умножить числитель и знаменатель дроби 3/4 (определить дополнительный множитель), чтобы знаменатель был равен 56, необходимо найти частное 56:4
56:4=14 - дополнительный множитель.
3/4=(3•14)/(4•14)=42/56
36/63=(4•9)/(7•9)=4/7
После сокращения дроби 36/63 получили равную ей дробь 4/7 .
Для того, чтобы определить, на какое число необходимо умножить числитель и знаменатель дроби 4/7 (определить дополнительный множитель), чтобы знаменатель был равен 56, необходимо найти частное 56:7
56:7=8 - дополнительный множитель.
4/7=(4•8)/(7•8)=32/56
Запишите в виде смешанного числа:
а) 31 : 9; б) 81 : 9; в) 402 : 15; г) 1429 : 14.
Черту обыкновенной дроби можно понимать как знак деления, то есть a/b=a:b.
Это правило работает и в обратном порядке, то есть
a:b=a/b
Необходимо представить число в смешанной записи (есть целая часть и дробная часть).
а) 31:9
Дробь 31/9 – неправильная, так как числитель 31 больше знаменателя 9.
Для того, чтобы из неправильной дроби выделить целую часть, необходимо разделить 31 на 9 с остатком
31:9=3 (ост.4)
Неполное частное (3) будет целой частью, остаток (4) даёт числитель, а делитель (9) – знаменатель дробной части
31:9=3 4/9
б) 81:9
Дробь 81/9 – неправильная, так как числитель 81 больше знаменателя 9.
Для того, чтобы из неправильной дроби выделить целую часть, необходимо разделить 81 на 9 с остатком
81:9=9 , то есть остатка нет.
Для того, чтобы представить число в смешанном виде, одну единицу запишем в виде неправильной дроби.
81:9=8 9/9
в) 402:15
Дробь 402/15 – неправильная, так как числитель 402 больше знаменателя 15.
Для того, чтобы из неправильной дроби выделить целую часть, необходимо разделить 402 на 15 с остатком
402:15=26 (ост.12)
Неполное частное (26) будет целой частью, остаток (12) даёт числитель, а делитель (15) – знаменатель дробной части
402:15=26 12/15=26 (12:3)/(15:3)=26 4/5
Если числитель и знаменатель дроби разделить на одно и то же натуральное число, то получится равная ей дробь.
г) 1429:14
Дробь 1429/14 – неправильная, так как числитель 1429 больше знаменателя 14.
Для того, чтобы из неправильной дроби выделить целую часть, необходимо разделить 1429 на 14 с остатком
1429:14=102 (ост.1)
Неполное частное (102) будет целой частью, остаток (1) даёт числитель, а делитель (14) – знаменатель дробной части
1429:14=102 1/14
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением