Упр.2.124 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
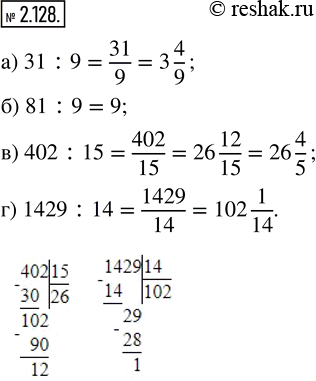
Решение #2 (Учебник 2023)
Решение #3 (Учебник 2023)
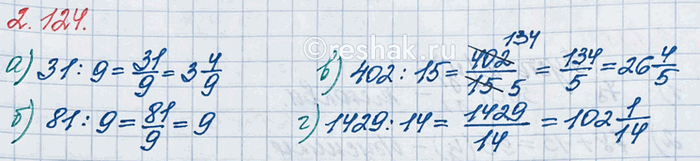
Решение #4 (Учебник 2021)
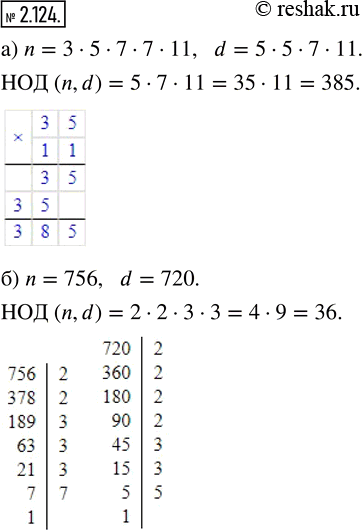
Решение #5 (Учебник 2021)
Решение #6 (Учебник 2021)
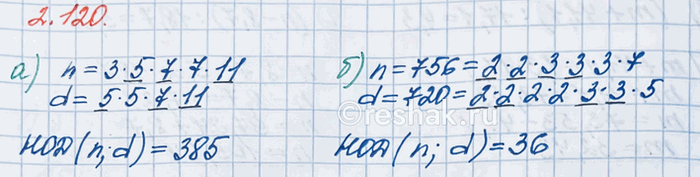
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Запишите в виде смешанного числа:
а) 31 : 9; б) 81 : 9; в) 402 : 15; г) 1429 : 14.
Черту обыкновенной дроби можно понимать как знак деления, то есть a/b=a:b.
Это правило работает и в обратном порядке, то есть
a:b=a/b
Необходимо представить число в смешанной записи (есть целая часть и дробная часть).
а) 31:9
Дробь 31/9 – неправильная, так как числитель 31 больше знаменателя 9.
Для того, чтобы из неправильной дроби выделить целую часть, необходимо разделить 31 на 9 с остатком
31:9=3 (ост.4)
Неполное частное (3) будет целой частью, остаток (4) даёт числитель, а делитель (9) – знаменатель дробной части
31:9=3 4/9
б) 81:9
Дробь 81/9 – неправильная, так как числитель 81 больше знаменателя 9.
Для того, чтобы из неправильной дроби выделить целую часть, необходимо разделить 81 на 9 с остатком
81:9=9 , то есть остатка нет.
Для того, чтобы представить число в смешанном виде, одну единицу запишем в виде неправильной дроби.
81:9=8 9/9
в) 402:15
Дробь 402/15 – неправильная, так как числитель 402 больше знаменателя 15.
Для того, чтобы из неправильной дроби выделить целую часть, необходимо разделить 402 на 15 с остатком
402:15=26 (ост.12)
Неполное частное (26) будет целой частью, остаток (12) даёт числитель, а делитель (15) – знаменатель дробной части
402:15=26 12/15=26 (12:3)/(15:3)=26 4/5
Если числитель и знаменатель дроби разделить на одно и то же натуральное число, то получится равная ей дробь.
г) 1429:14
Дробь 1429/14 – неправильная, так как числитель 1429 больше знаменателя 14.
Для того, чтобы из неправильной дроби выделить целую часть, необходимо разделить 1429 на 14 с остатком
1429:14=102 (ост.1)
Неполное частное (102) будет целой частью, остаток (1) даёт числитель, а делитель (14) – знаменатель дробной части
1429:14=102 1/14
Найдите НОД (n, d) если:
а) n = 3 · 5 · 7 · 7 · 11, d = 5 · 5 · 7 · 11; б) n = 756, d = 720.
Наибольшим общим делителем (НОД) нескольких чисел называют наибольшее натуральное число, на которое делятся эти числа без остатка.
Для того, чтобы найти наибольший общий делитель нескольких натуральных чисел, необходимо:
- разложить их на простые множители;
- из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые входят в разложение других чисел;
- найти произведение этих множителей.
а) n=3•5•7•7•11
d=5•5•7•11
НОД (n,d)=5•7•11=35•11=385
б) n=756, d=720
n=2•2•3•3•3•7
d=2•2•2•2•3•3•5
НОД (n,d)=2•2•3•3=4•9=36
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением