Упр.1340 ГДЗ Атанасян 7-9 класс по геометрии (Геометрия)
Решение #1 (Учебник 2025)
Рассмотрим вариант решения задания из учебника Атанасян, Бутузов 9 класс, Просвещение:
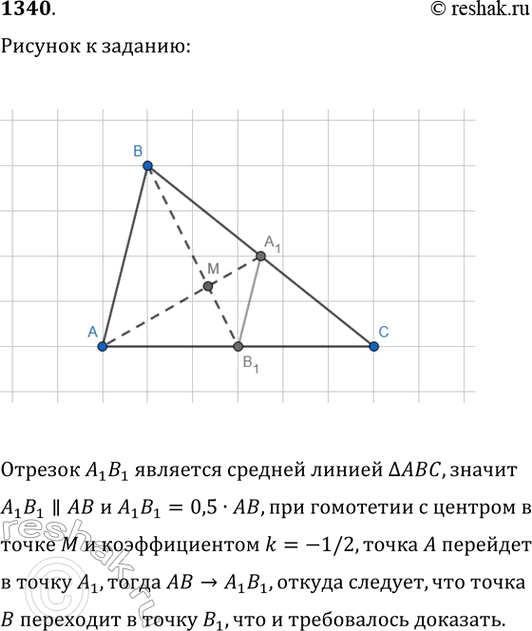
1340. Пусть М — точка, делящая медиану AA_1 треугольника АВС в отношении 2:1, считая от вершины, B_1 — середина стороны АС треугольника. Докажите, не используя свойство медиан, что при гомотетии с центром в точке М и коэффициентом k=-1/2 отрезок АВ переходит в отрезок A_1B_1, причём точка А переходит в точку A_1, а точка В — в точку B_1.
Отрезок A_1 B_1 является средней линией треугольника ABC,значит A_1 B_1 || AB и A_1 B_1=0,5•AB, при гомотетии с центром в точке M и коэффициентом k=-1/2,точка A перейдет в точку A_1,тогда AB>A_1 B_1,откуда следует, что точка B переходит в точку B_1,что и требовалось доказать.
Похожие решебники
Популярные решебники 9 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.