Тест Глава 4 ГДЗ Мордкович Семенов 11 класс (Алгебра)
Решение #1
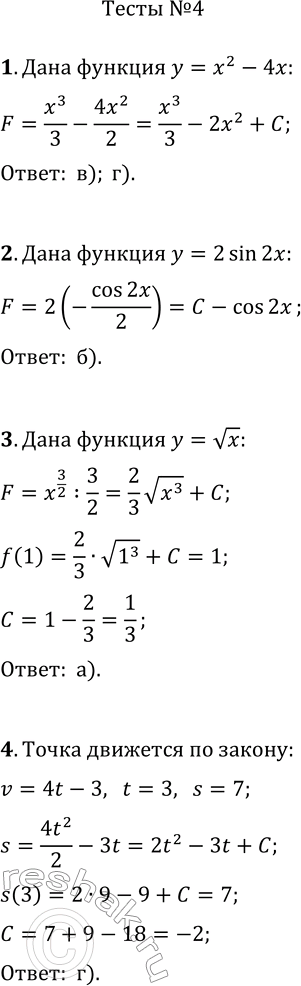



Рассмотрим вариант решения задания из учебника Мордкович, Семенов, Александрова 11 класс, Просвещение:
1. Укажите функции, которые являются первообразными для функции y=x^2-4x.
а) y=2x-4; в) y=(1/3)x^3-2x^2+4;
б) y=3x^3-8x^2; г) y=(x^3-1)/3-2x^2.
2. Укажите функцию, которая является первообразной для функции y=2sin(2x).
а) y=cos(2x)-1; в) y=-4cos(2x);
б) y=2-cos(2x); г) y=1-2cos(2x).
3. Укажите функцию y=F(x), которая является первообразной для функции y=vx, если известно, что F(1)=1.
а) F(x)=(2xvx+1)/3; в) F(x)=2/vx-1;
б) F(x)=1/(2vx)+1/2; г) F(x)=(3xvx-1)/2.
4. Точка движется по координатной прямой со скоростью, заданной формулой v=4t-3. Найдите закон движения s=s(t), если известно, что в момент времени t=3 координата точки s=7.
а) s=2t^2-3t-5; в) s=4t^2-3t-20;
б) s=2t^2-12; г) s=2t^2-3t-2.
5. Найдите множество всех первообразных функции y=e^(2x-3)+1/(3x).
а) y=e^(2x-3)+ln(3x)+C; в) y=2e^(2x-3)+3ln(3x)+C;
б) y=(1/2)e^(2x-3)+(1/3)ln(x)+C; г) y=(1/2)e^x+(1/3)ln(x)+C.
6. Вычислите: (-1,1)?(x^3-1/x^2+1)dx.
7. Установите соответствие между определённым интегралом и его значением.
А. (?/3,?/2)?sin(2x)dx; Б. (?/3,?)?cos(x/2)dx; В. (-?/8,?/8)?(2/cos^2(2x))dx;
1) 2; 2) 1; 3) 0; 4) 0,25.
8. Не производя вычислений, укажите интеграл с наименьшим значением.
а) (-1,1)?(x+4)^(1/3)dx; в) (1,3)?(x+4)^(1/3)dx;
б) (1,2)?(x+4)^(1/3)dx; г) (2,3)?(x+4)^(1/3)dx.
9. Найдите площадь криволинейной трапеции, ограниченной графиком функции y=3x^2-2x+5 и прямыми x=1, x=3, y=0.
10. Найдите площадь фигуры, ограниченной графиками функций y=x^3+3x^2, y=4/x^2 и прямыми x=2, y=0.
Похожие решебники
Популярные решебники 11 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением







