Упр.91 ГДЗ Мерзляк Полонский 6 класс (Математика)
Решение #1
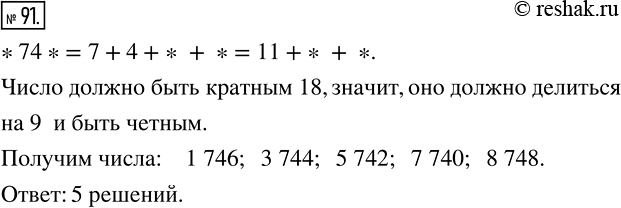
Решение #2
Рассмотрим вариант решения задания из учебника Мерзляк, Полонский, Якир 6 класс, Вентана-Граф:
91 Вместо звездочек поставьте такие цифры, чтобы четырехзначное число *74* делилось нацело на 18. Найдите все решения.
Так как 18=9•2, то число будет делиться нацело на 18, если оно кратно 9 и кратно 2 одновременно.
Пусть искомое число выглядит так: x74y.
x – первая цифра числа, y – последняя.
По условию, число должно быть кратно 18. Значит, на последнем месте может быть только четная цифра.
Так как оно должно делиться нацело на 2, то по признаку делимости на 2, число оканчивается цифрой 0, 2, 4, 6 или 8.
Рассмотрим каждый случай отдельно.
1) Если y=0.
Число x740 должно быть кратно 9.
Сумма цифр числа равна x+7+4+0=x+11.
Подбираем цифру x так, чтобы эта сумма была кратна 9. Цифру 0 не рассматриваем, так как ее нельзя записать на первом месте. Возможен только один вариант: 7+11=18
Значит, x=7.
Получим число: 7740.
2) Если y=2.
Число x742 должно быть кратно 9.
Сумма цифр числа равна x+7+4+2=x+13.
Подбираем цифру x так, чтобы эта сумма была кратна 9. Возможен только один вариант: 5+13=18
Значит, x=5.
Получим число: 5742.
3) Если y=4.
Число x744 должно быть кратно 9.
Сумма цифр числа равна x+7+4+4=x+15.
Подбираем цифру x так, чтобы эта сумма была кратна 9. Возможен только один вариант: 3+15=18
Значит, x=3.
Получим число: 3744.
4) Если y=6.
Число x746 должно быть кратно 9.
Сумма цифр числа равна x+7+4+6=x+17.
Подбираем цифру x так, чтобы эта сумма была кратна 9. Возможен только один вариант: 1+17=18
Значит, x=1.
Получим число: 1746.
5) Если y=8.
Число x748 должно быть кратно 9.
Сумма цифр числа равна x+7+4+8=x+19.
Подбираем цифру x так, чтобы эта сумма была кратна 9. Возможен только один вариант: 8+19=27
Значит, x=8.
Получим число: 8748.
Ответ: 7740, 5742, 3744, 1746 и 8748 – 5 решений.
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением
