Упр.863 ГДЗ Мерзляк 9 класс (Алгебра)
Решение #1 (Учебник 2024)
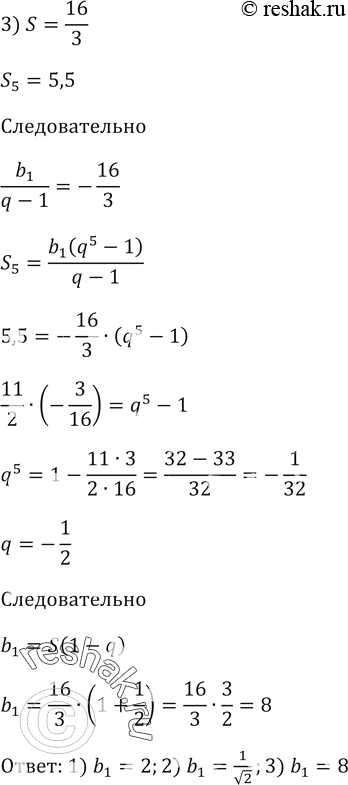
Решение #2 (Учебник 2024)
Решение #3 (Учебник 2021)
Решение #4 (Учебник 2021)
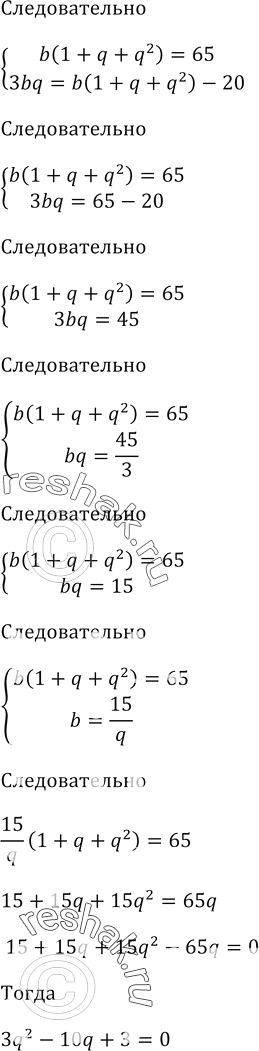
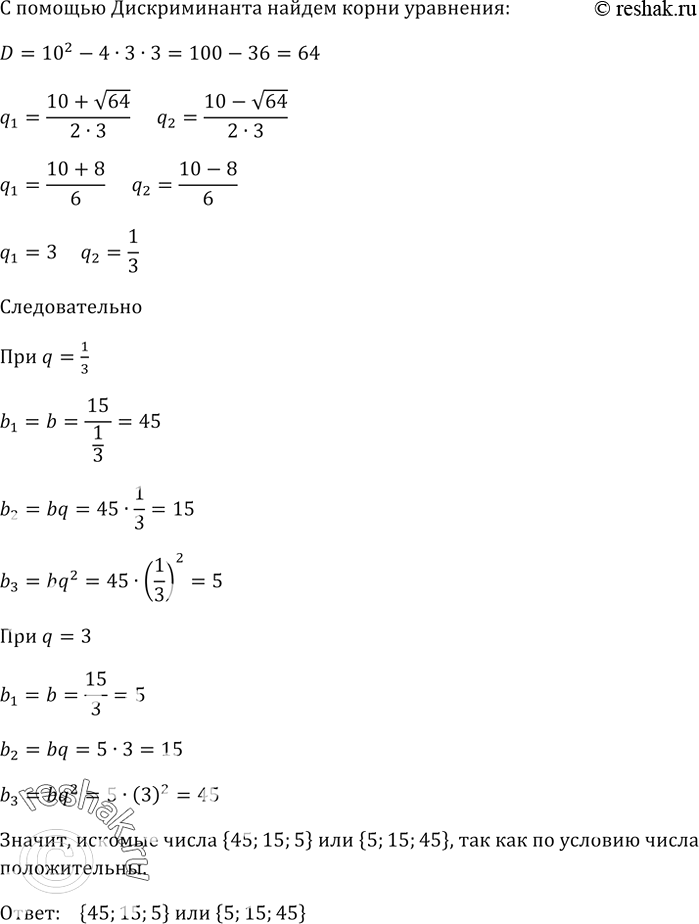
Рассмотрим вариант решения задания из учебника Мерзляк, Полонская, Якир 9 класс, Просвещение:
Найдите первый член бесконечной геометрической прогрессии, если:
1) сумма прогрессии равна 4, а знаменатель равен 1/2;
2) сумма прогрессии равна корень(2) + 1, а знаменатель равен корень(2)/2;
3) сумма прогрессии равна 16/3, а сумма пяти первых членов равна 5,5.
Сумма трёх чисел, образующих геометрическую прогрессию, равна 65.
Если из первого из этих чисел вычесть 1, из третьего вычесть 19, а второе оставить без изменений, то полученные числа образуют арифметическую прогрессию. Найдите данные числа.
Похожие решебники
Популярные решебники 9 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением