Упр.859 ГДЗ Мерзляк 9 класс (Алгебра)
Решение #1 (Учебник 2024)

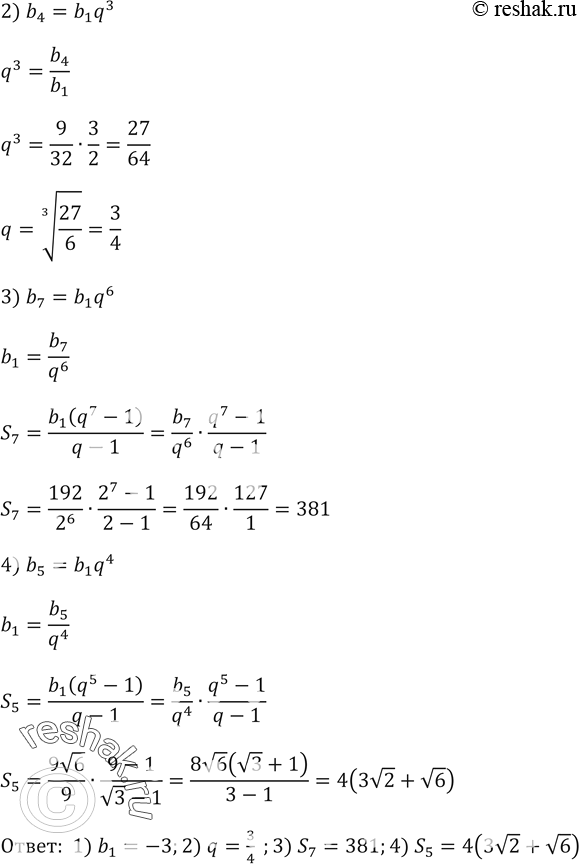
Решение #2 (Учебник 2024)

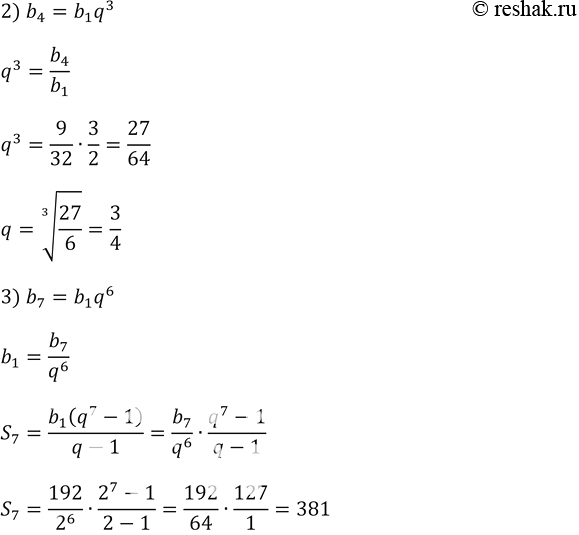
Решение #3 (Учебник 2021)

Решение #4 (Учебник 2021)


Рассмотрим вариант решения задания из учебника Мерзляк, Полонская, Якир 9 класс, Просвещение:
Дана геометрическая прогрессия (bn) со знаменателем q. Найдите:
1) b1, если b5 = - 16/17, q = -2/3;
2) q, если b1 = 2/3, b4 = 9/32;
3) сумму семи первых членов прогрессии, если b7 = 192, q = 2;
4) сумму пяти первых членов прогрессии, если b5 = 9корень(6), q = корень(3).
Докажите, что если члены последовательности (bn) отличны от нуля и при любом натуральном n > 1 выполняется равенство bn^2 = b(n -1) * b(n + 1), то последовательность (bn) является геометрической прогрессией.
Похожие решебники
Популярные решебники 9 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.










