Упр.5.34 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
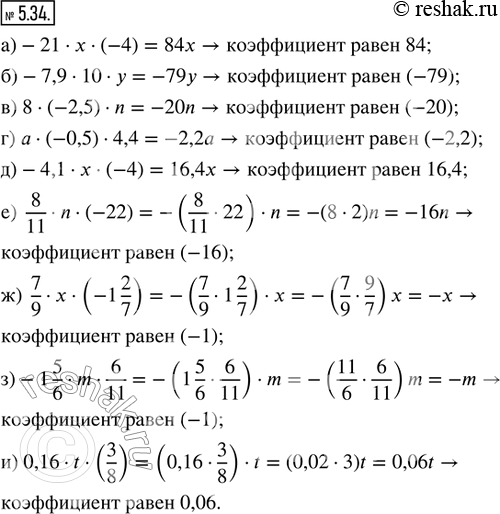
Решение #2 (Учебник 2023)
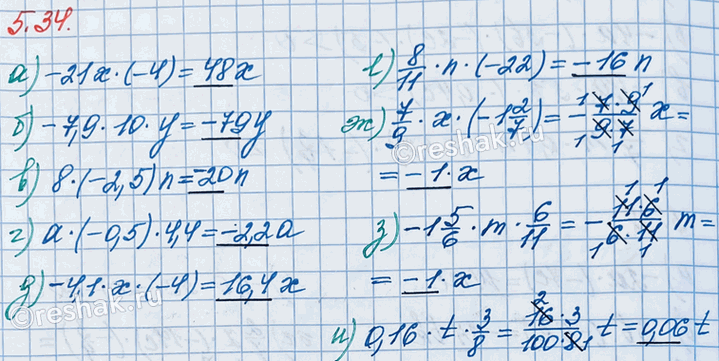
Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Упростите выражение и назовите его коэффициент:
а) -21 · x · (-4); г) а · (-0,5) · 4,4; ж) 7/9 · x · (-1 2/7);
б) -7,9 · 10 · у; д) -4,1 · x · (-4); з) -1 5/6 · m · 6/11;
в) 8 · (-2,5) · n; е) 8/11 · n · (-22); и) 0,16 · t · (3/8).
В каждом произведении используем переместительное и сочетательное свойства умножения рациональных чисел, то есть множители в произведениях меняем местами и расставляем скобки так, чтобы можно было выполнить умножение чисел, имеющихся в произведениях, и в каждом случае получаем число и произведение одной или нескольких букв, полученное число называется числовым коэффициентом или просто коэффициентом.
При выполнении умножения опираемся на следующие правила:
- для того, чтобы перемножить два числа с разными знаками, необходимо умножить их модули и перед полученным произведением поставить знак «-».
- для того, чтобы перемножить два отрицательных числа, необходимо перемножить их модули.
- для того, чтобы умножить десятичную дробь на натуральное число, необходимо умножить их как натуральные числа, не обращая внимание на запятую; в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятой у умножаемой дроби.
- произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
- для того, чтобы выполнить умножение смешанных чисел, необходимо записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
- для того, чтобы преобразовать смешанное число в неправильную дробь, необходимо целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в её знаменатель записать знаменатель дробной части смешанного числа.
Также при умножении обыкновенных дробей, если возможно, выполняем сокращение.
а) -21•x•(-4)=-21•(-4)•x=21•4•x=84x
Коэффициент равен 84.
б) -7,9•10•y=-79y
Коэффициент равен -79.
в) 8•(-2,5)•n=-20n
Коэффициент равен -20.
г) a•(-0,5)•4,4=-0,5•4,4•a=-2,2a
Коэффициент равен -2,2.
д) -4,1•x•(-4)=-4,1•(-4)•x=4,1•4•x=16,4x
Коэффициент равен 16,4.
е) 8/11•n•(-22)=8/11•(-22)•n=-(8•22)/11•n=-(8•2•11)/11•n=-16n
Коэффициент равен -16.
ж) 7/9•x•(-1 2/7)=7/9•(-1 2/7)•x=7/9•(-9/7)•x=-(7•9)/(9•7)•x=-1x==-x
Коэффициент равен -1.
з) -1 5/6•m•6/11=-1 5/6•6/11•m=-11/6•6/11•m=-(11•6)/(6•11)•m=-1m==-m
Коэффициент равен -1.
и) 0,16•t•3/8=0,16•3/8•t=16/100•3/8•t=(16•3)/(100•8)•t=(2•8•3)/(100•8)•t=6/100 t==0,06t
Коэффициент равен 0,06.
Похожие решебники
Популярные решебники 6 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением