Упр.4.75 ГДЗ Виленкин Жохов 6 класс Часть 2, Просвещение (Математика)
Решение #1 (Учебник 2023)
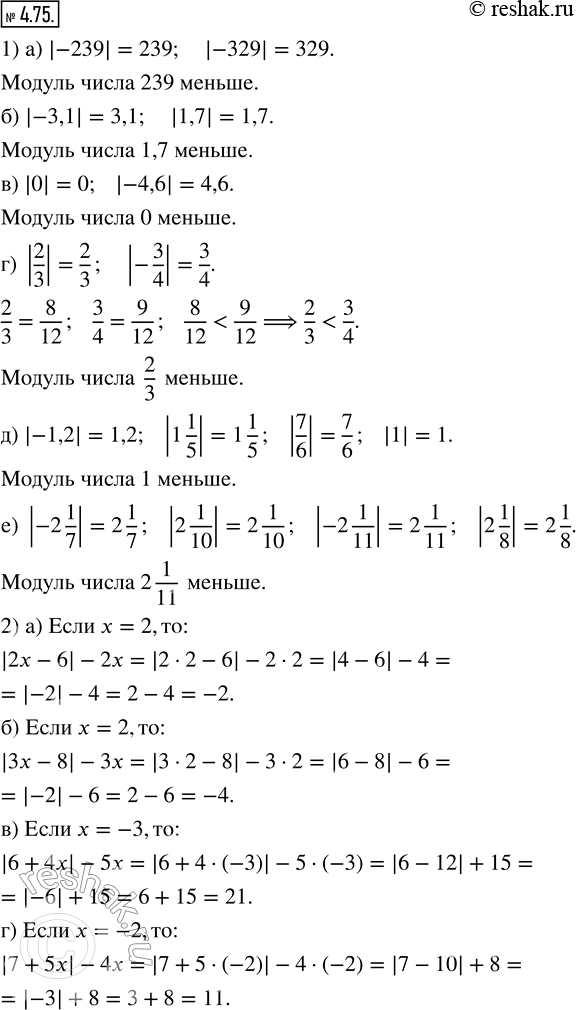
Решение #2 (Учебник 2023)

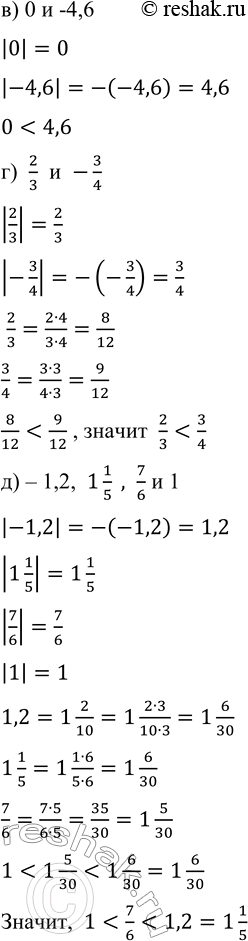
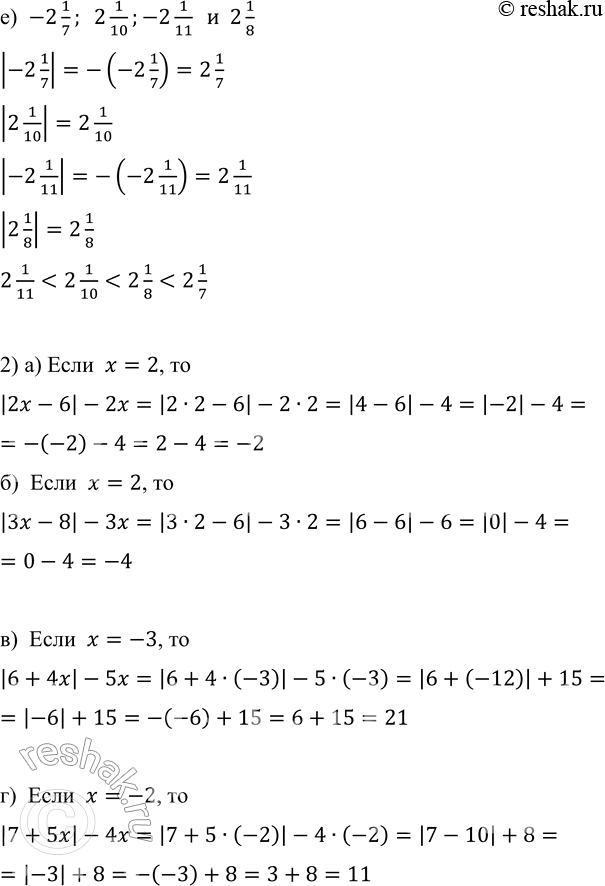
Решение #3 (Учебник 2023)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
) Из чисел выберите то, модуль которого меньше.
а) -239 и -329; в) 0 и -4,6; д) -1,2, 1 1/5, 7/6 и 1;
б) -3,1 и 1,7; г) 2/3 и -3/4; е) -2 1/7, 2 1/10, -2 1/11 и 2 1/8.
а) – 239 и -329
|-239|=-(-239)=239
|-329|=-(-329)=329
239<329
б) – 3,1 и 1,7
|-3,1|=-(-3,1)=3,1
|1,7|=1,7
3,1>1,7
в) 0 и -4,6
|0|=0
|-4,6|=-(-4,6)=4,6
0<4,6
г) 2/3 и -3/4
|2/3|=2/3
|-3/4|=-(-3/4)=3/4
2/3=(2•4)/(3•4)=8/12
3/4=(3•3)/(4•3)=9/12
8/12<9/12 , значит 2/3<3/4
д) – 1,2, 1 1/5 , 7/6 и 1
|-1,2|=-(-1,2)=1,2
|1 1/5|=1 1/5
|7/6|=7/6
|1|=1
1,2=1 2/10=1 (2•3)/(10•3)=1 6/30
1 1/5=1 (1•6)/(5•6)=1 6/30
7/6=(7•5)/(6•5)=35/30=1 5/30
1<1 5/30<1 6/30=1 6/30
Значит, 1<7/6<1,2=1 1/5
е) -2 1/7; 2 1/10;-2 1/11 и 2 1/8
|-2 1/7|=-(-2 1/7)=2 1/7
|2 1/10|=2 1/10
|-2 1/11|=-(-2 1/11)=2 1/11
|2 1/8|=2 1/8
2 1/11<2 1/10<2 1/8<2 1/7
2) Найдите значение выражения:
а) |2x - 6| - 2x при х = 2; в) |6 + 4x| - 5x при х = -3;
б) |3x - 8| - 3x при х = 2; г) |7 + 5x| - 4x при х = -2.
а) Если x=2, то
|2x-6|-2x=|2•2-6|-2•2=|4-6|-4=|-2|-4=-(-2)-4=2-4=-2
б) Если x=2, то
|3x-8|-3x=|3•2-6|-3•2=|6-6|-6=|0|-4=0-4=-4
в) Если x=-3, то
|6+4x|-5x=|6+4•(-3)|-5•(-3)=|6+(-12)|+15=|-6|+15=-(-6)+15=6+15=21
г) Если x=-2, то
|7+5x|-4x=|7+5•(-2)|-4•(-2)=|7-10|+8=|-3|+8=-(-3)+8=3+8=11
Модулем числа a называют расстояние (в единичных отрезках) от начала координат до точки А (a).
Обозначают: |a| (читают «модуль a»).
Модуль числа не может быть отрицательным.
Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу.
Противоположные числа имеют равные модули.
|a|=a, если a - неотрицательное число.
|a|=-a, если a - отрицательное число.
|a|=|-a|.
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.