Упр.4.52 ГДЗ Погорелов 7-9 класс (Геометрия)
Решение #1
Рассмотрим вариант решения задания из учебника Погорелов 7 класс, Просвещение:
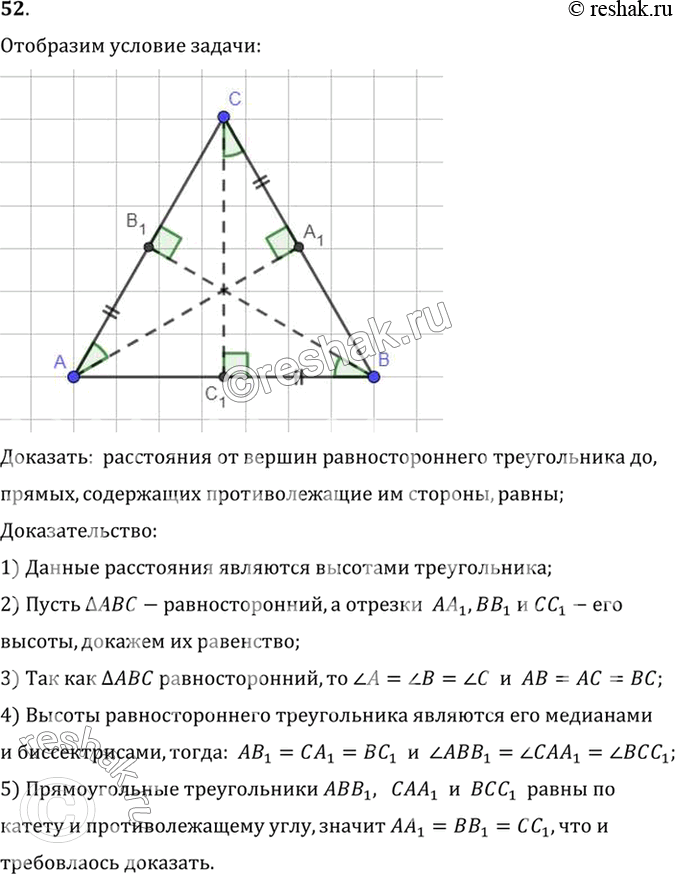
52. Докажите, что расстояния от вершин равностороннего треугольника до прямых, содержащих противолежащие им стороны, равны.
Доказать: расстояния от вершин равностороннего треугольника до,
прямых, содержащих противолежащие им стороны, равны;
Доказательство:
1) Данные расстояния являются высотами треугольника;
2) Пусть треугольник ABC-равносторонний, а отрезки AA1, BB1 и CC1-его
высоты, докажем их равенство;
3) Так как треугольник ABC равносторонний, то угол A = углу B = углу C и AB=AC=BC;
4) Высоты равностороннего треугольника являются его медианами
и биссектрисами, тогда: AB1=CA1=BC1 и угол ABB1 = углу CAA1 = углу BCC1;
5) Прямоугольные треугольники ABB1, CAA1 и BCC1 равны по
катету и противолежащему углу, значит AA1=BB1=CC1, что и
требовлаось доказать.
Популярные решебники 7 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением





