Упр.4.2 ГДЗ Погорелов 7-9 класс (Геометрия)
Решение #1
Рассмотрим вариант решения задания из учебника Погорелов 7 класс, Просвещение:
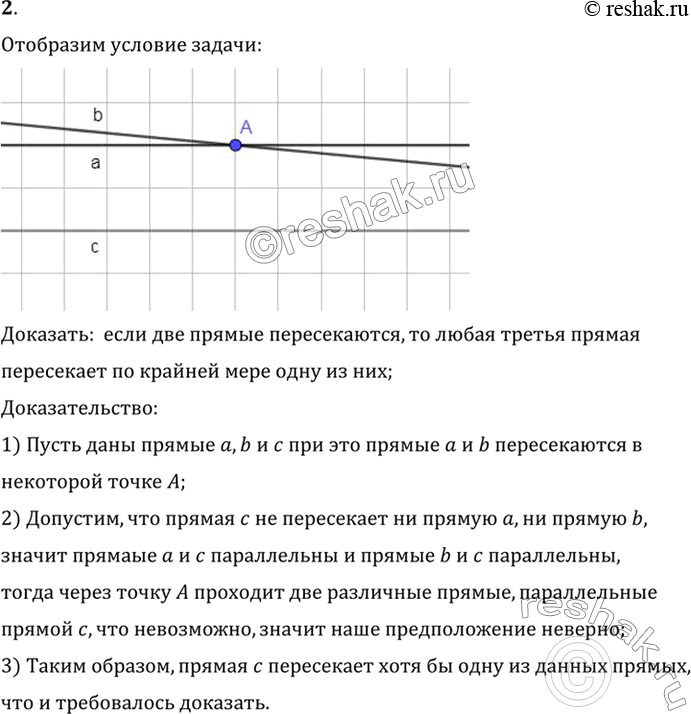
2. Докажите, что если две прямые пересекаются, то любая третья прямая пересекает по крайней мере одну из этих прямых.
Доказать: если две прямые пересекаются, то любая третья прямая
пересекает по крайней мере одну из них;
Доказательство:
1) Пусть даны прямые a, b и c при это прямые a и b пересекаются в
некоторой точке A;
2) Допустим, что прямая c не пересекает ни прямую a, ни прямую b,
значит прямаые a и c параллельны и прямые b и c параллельны,
тогда через точку A проходит две различные прямые, параллельные
прямой c, что невозможно, значит наше предположение неверно;
3) Таким образом, прямая c пересекает хотя бы одну из данных прямых,
что и требовалось доказать.
Популярные решебники 7 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением