Упр.3.89 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
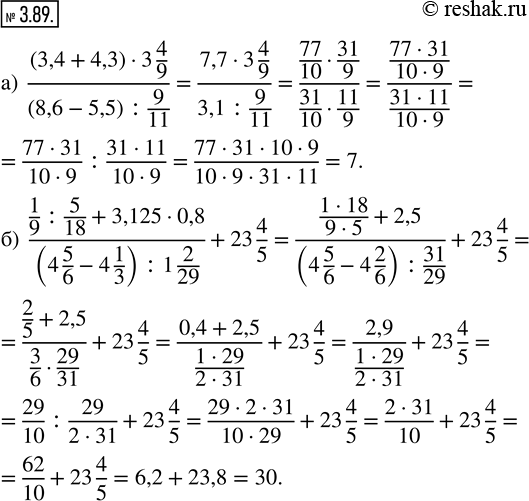
Решение #2 (Учебник 2023)


Решение #3 (Учебник 2023)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Выполните действия:
а) ((3,4 + 4,3) · 3 4/9)/((8,6 - 5,5) : 9/11);
б) (1/9 : 5/18 + 3,125 · 0,8)/((4 5/6 - 4 1/3) : 1 2/29) + 23 4/5.
Для того, чтобы найти значения представленных выражений, отдельно находим значение выражения, стоящего в числителе дробного выражения, далее находим значение выражения, стоящего в знаменателе дробного выражения, и затем, находим отношение полученных значений.
При выборе порядка выполнения действий в числителе и знаменателе дробных выражений, опираемся на следующие правила:
- если в выражении нет скобок и оно содержит действия первой (сложение и вычитание) и второй (умножение и деление) ступени, то сначала выполняют действия второй ступени по порядку слева направо, а потом действия первой ступени, также по порядку слева направо.
- если в выражении есть скобки, то сначала выполняют действия в скобках, при этом, как в скобках, так и за скобками, сначала выполняют действия второй ступени (умножение и деление) по порядку слева направо, а потом действия первой ступени (сложение и вычитание), также по порядку слева направо.
При выполнении вычислений опираемся на следующие правила:
- для того, чтобы перемножить две десятичные дроби, необходимо умножить их как натуральные числа, не обращая внимание на запятые; в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
- для того, чтобы выполнить вычитание смешанных чисел, необходимо отдельно выполнить вычитание целых частей, и отдельно вычитание дробных частей чисел.
- прежде, чем выполнить вычитание обыкновенных дробей, необходимо привести их к одинаковому знаменателю.
- разность дробей с одинаковыми знаменателями равна дроби, числитель которой равен разности числителей, а знаменатель оставляем без изменений.
а) ((3,4+4,3)•3 4/9)/((8,6-5,5):9/11)=(7,7•31/9)/(3,1•11/9)=(77/10•31/9)/(31/10•11/9)=(77•31)/(10•9) :(31•11)/(10•9)=(77•31)/(10•9)•(10•9)/(31•11)=(77•31•10•9)/(10•9•31•11)=(7•11)/11=7/1=7
б) (1/9 :5/18+3,125•0,8)/((4 5/6-4 1/3) :1 2/29)+23 4/5=(1/9•18/5+2,5000)/((4 5/6-4 (1•2)/(3•2)) :31/29)+23 4/5=((1•18)/(9•5)+2,5)/((4 5/6-4 2/6)•29/31)+23 4/5=((2•9)/(9•5)+2,5)/(((4-4)+(5/6-2/6))•29/31)+23 4/5=((2•2)/(5•2)+2,5)/((0+(5-2)/6)•29/31)+23 4/5=(4/10+2,5)/(3/6•29/31)+23 4/5=(0,4+2,5)/(3/(2•3)•29/31)+23 4/5=2,9/(29/(2•31))+23 4/5=(29/10)/(29/62)+23 (4•2)/(5•2)=29/10 :29/62+23 8/10=29/10•62/29+23,8=(29•62)/(10•29)+23,8=62/10+23,8=6,2+23,8=30,0==30
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









