Упр.2.271 ГДЗ Виленкин Жохов 6 класс Часть 1, Просвещение (Математика)
Решение #1 (Учебник 2023)
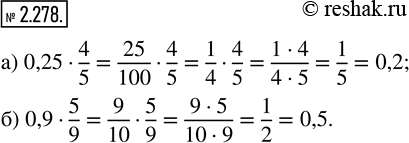
Решение #2 (Учебник 2023)

Решение #3 (Учебник 2023)

Решение #4 (Учебник 2021)
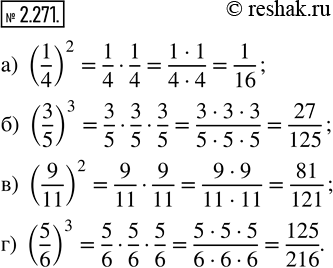
Решение #5 (Учебник 2021)

Решение #6 (Учебник 2021)

Рассмотрим вариант решения задания из учебника Виленкин, Жохов, Чесноков 6 класс, Просвещение:
Представьте десятичную дробь в виде обыкновенной и выполните умножение:
а) 0,25 · 4/5; 6) 0,9 · 5/9.
а) 0,25•4/5
Для того, чтобы 0,25 перевести в обыкновенную дробь, в числителе дроби записываем число, стоящее после запятой (25), а в знаменателе 1 и столько же нулей, сколько знаков после запятой в десятичной дроби 0,25 (два знака), получим
0,25=25/100
Сократим получившуюся дробь на 25.
25/100=25/(25•4)=1/4
0,25•4/5=1/4•4/5=(1•4)/(4•5)=1/5=0,2
б) 0,9•5/9
Для того, чтобы 0,9 перевести в обыкновенную дробь, в числителе дроби записываем число, стоящее после запятой (9), а в знаменателе 1 и столько же нулей, сколько знаков после запятой в десятичной дроби 0,9 (один знак), получим
0,9=9/10
0,9•5/9=9/10•5/9=(9•5)/(10•9)=(9•5)/(5•2•9)=1/2=0,5
Выполните действие:
а) (1/4)^2; б) (3/5)^3; в) (9/11)^2; г) (5/6)^3.
При возведении в степень, дробь необходимо умножить саму на себя столько раз, какова степень дроби, а далее выполнять умножение дробей согласно правилу.
Для того, чтобы умножить дробь на дробь, необходимо найти произведение числителей и знаменателей этих дробей. Первое произведение записать числителем, второе – знаменателем.
При умножении необходимо выполнять сокращение, если это возможно, для удобства расчётов. Для этого необходимо одно из чисел числителя и знаменателя разделить на одно и то же число и далее выполнять умножение.
а) (1/4)^2=1/4•1/4=(1•1)/(4•4)=1/16
б) (3/5)^3=3/5•3/5•3/5=(3•3•3)/(5•5•5)=27/125
в) (9/11)^2=9/11•9/11=(9•9)/(11•11)=81/121
г) (5/6)^3=5/6•5/6•5/6=125/216
Похожие решебники
Популярные решебники 6 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.









