Упр.801 ГДЗ Мерзляк Полонский 5 класс (Математика)
Решение #1 (Учебник 2024)
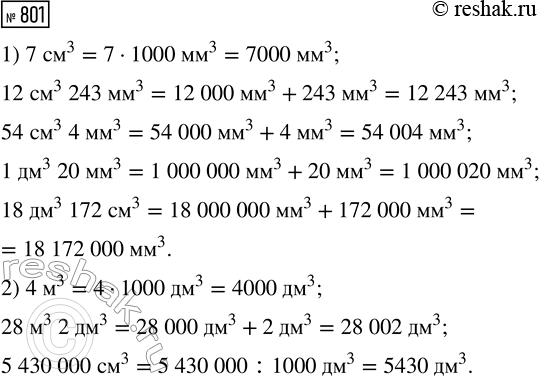
Решение #2 (Учебник 2024)




Решение #3 (Учебник 2019)
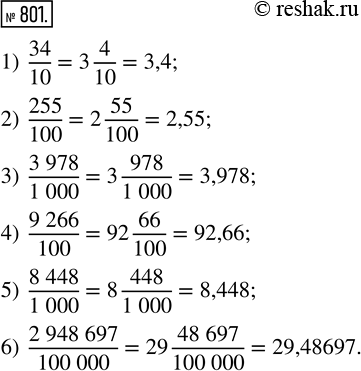
Решение #4 (Учебник 2019)



Рассмотрим вариант решения задания из учебника Мерзляк, Полонский, Якир 5 класс, Просвещение:
Выразите:
1) в кубических миллиметрах: 7 см^3; 12 см^3 243 мм^3; 54 см^3 4 мм^3; 1 дм^3 20 мм^3; 18 дм^3 172 см^3;
2) в кубических дециметрах: 4 м^3; 28 м^3 2 дм^3; 5 430 000 см^3.
Выделите целую и дробную части числа и запишите данное число в виде десятичной дроби:
1) 34/10; 3) 3978/1000; 5) 8448/1000;
2) 255/100; 4) 9266/100; 6) 2948697/100000.
Для того, чтобы неправильную дробь, числитель которой нацело не делится на знаменатель, преобразовать в смешанное число, необходимо числитель разделить на знаменатель; полученное неполное частное записать как целую часть смешанного числа, а остаток – как числитель его дробной части.
Затем полученное смешанное число записать в виде десятичной дроби, опираясь на правило, согласно которому при записи обыкновенной дроби в виде десятичной, после запятой стоит столько цифр, сколько нулей стоит в записи знаменателя соответствующей обыкновенной дроби.
1) Разделим с остатком 34 (числитель) на 10 (знаменатель).
34:10=3 (ост. 4)
34=3•10+4
34/10=3 4/10
В записи знаменателя (10) один ноль, значит, в записи дробной части десятичной дроби должна быть одна цифра.
3 4/10=3,_
В записи числа 4 также одна цифра, поэтому просто пишем 4 в десятые.
34/10=3 4/10=3,4
2) 255:100=2 (ост. 55)
255/100=2 55/100=2,55
3) 3 978:1 000=3 (ост. 978)
(3 978)/(1 000)=3 978/(1 000)=3,978
4) 9 266:100=92 (ост. 66)
(9 266)/100=92 66/100=92,66
5) 8 488:1 000=8 (ост. 488)
(8 448)/(1 000)=8 488/(1 000)=8,448
6) 2 948 697:100 000=29 (ост. 48 697)
(2 948 697)/(100 000)=29 (48 697)/(100 000)=29,48697
Десятичная дробь получается так, что берётся число из числителя и в нём ставится запятая так, чтобы после запятой было столько цифр, сколько нулей стоит в знаменателе соответствующей обыкновенной дроби.
Похожие решебники
Популярные решебники 5 класс Все решебники
*К сожалению, временные проблемы с публикацией комментариев с мобильных устройств.







