Упр.761 ГДЗ Колягин Ткачёва 9 класс (Алгебра)
Решение #1

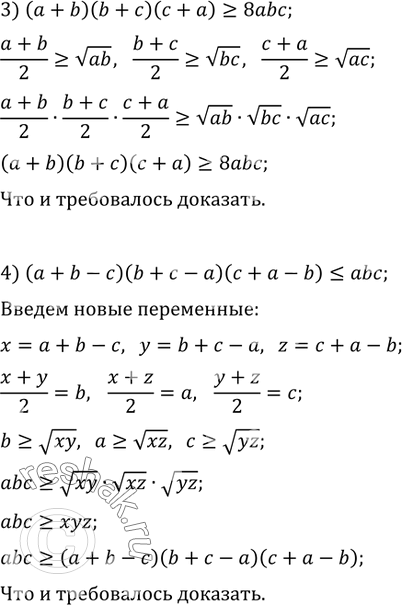

Рассмотрим вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 9 класс, Просвещение:
761. Доказать, что для любых неотрицательных чисел a, b, c справедливо неравенство:
1) a^3+b^3+c^3?3abc;
2) (a+b+c)(ab+bc+ca)?9abc;
3) (a+b)(b+c)(c+a)?8abc;
4) (a+b-c)(b+c-a)(c+a-b)?abc.
Популярные решебники 9 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением





