Упр.755 ГДЗ Мерзляк 9 класс (Алгебра)
Решение #1 (Учебник 2024)
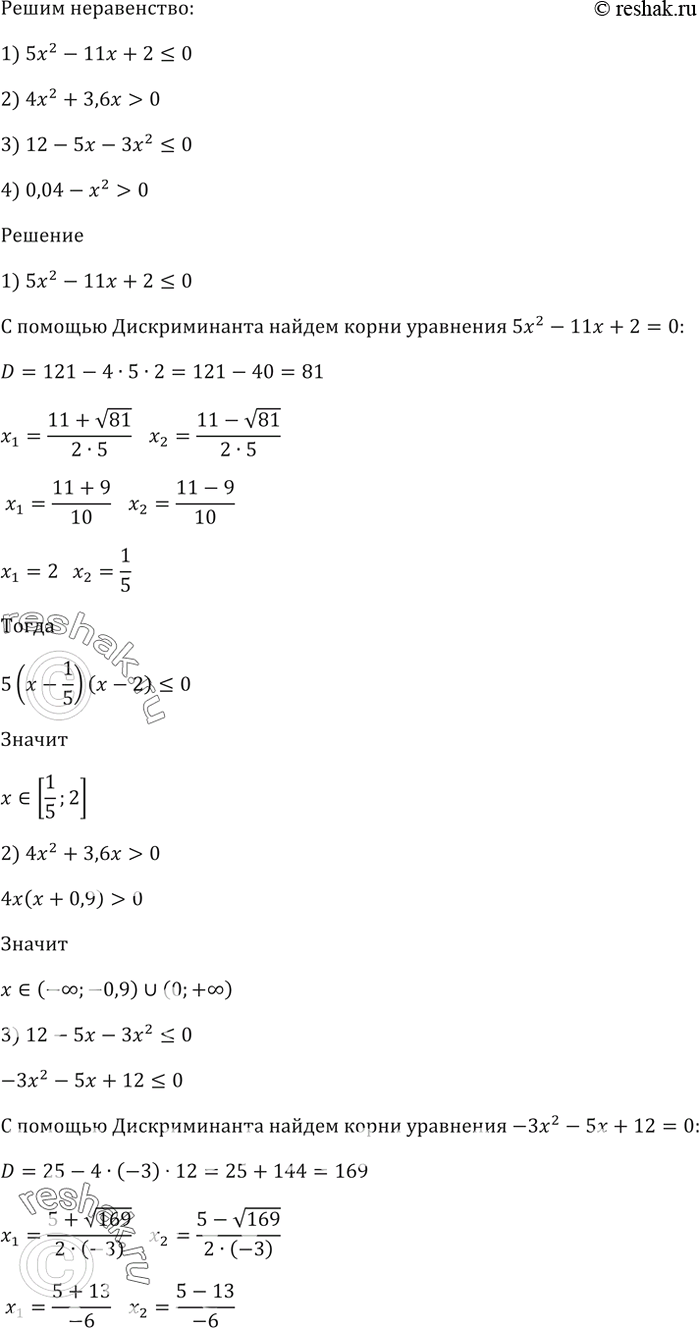
Решение #2 (Учебник 2024)
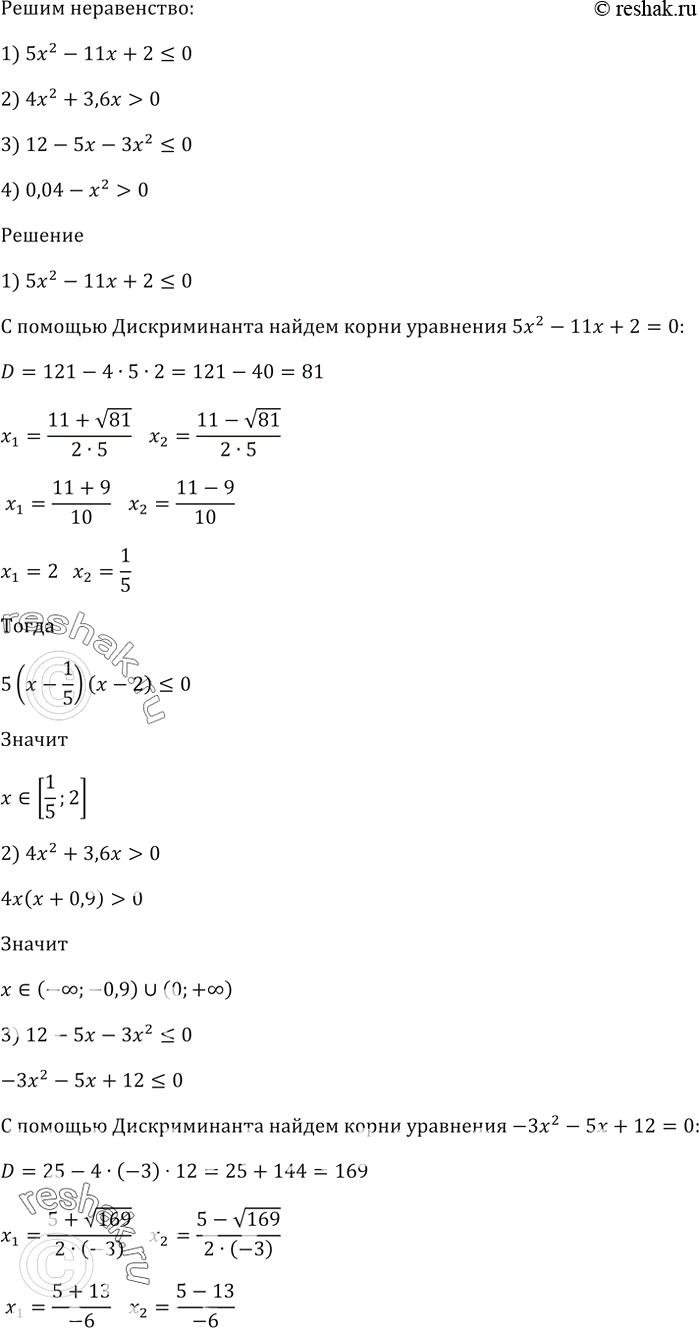
Решение #3 (Учебник 2021)
Решение #4 (Учебник 2021)
Рассмотрим вариант решения задания из учебника Мерзляк, Полонская, Якир 9 класс, Просвещение:
Решите неравенство:
1) 5х^2- 11x + 2 <= 0;
2) 4х^2 + 3,6х > 0;
3) 12 - 5х - Зх^2 <= 0;
4) 0,04 — х^2 > 0.
Докажите, что если положительные числа а, b и с — три последовательных члена арифметической прогрессии, то
1/((корень(а) + корень(b)) + 1/((корень(b) + корень(c)) = 2/((корень(а) + корень(c)).
Похожие решебники
Популярные решебники 9 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением