Упр.445 ГДЗ Никольский Потапов 7 класс (Алгебра)
Решение #1
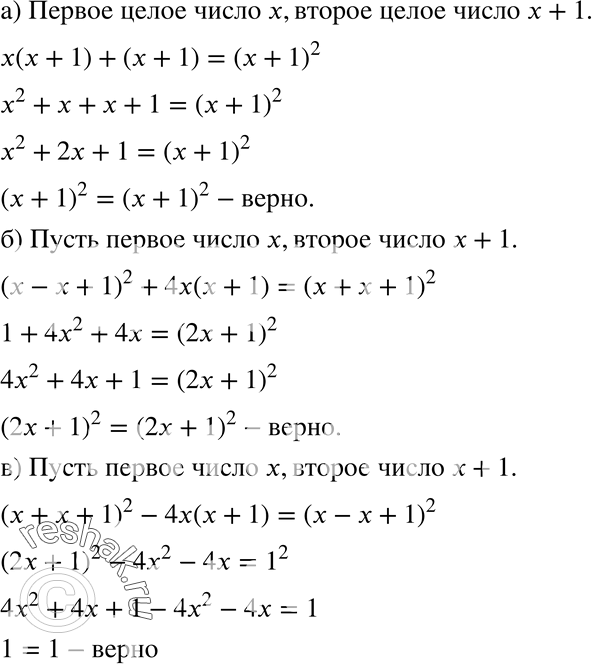
Решение #2
Рассмотрим вариант решения задания из учебника Никольский, Потапов 7 класс, Просвещение:
445. Докажите, что:
а) если к произведению двух целых последовательных чисел прибавить большее из них, то получится квадрат большего числа;
б) сумма квадрата разности двух чисел и их учетверённого произведения равна квадрату суммы этих чисел;
в) разность квадрата суммы двух чисел и их учетверённого произведения равна квадрату разности этих чисел.
а) Пусть первое целое число равно x, тогда второе целое число равно x+1.
x(x+1)+(x+1)=(x+1)^2
x^2+x+x+1=(x+1)^2
x^2+2x+1=(x+1)^2
(x+1)^2=(x+1)^2 – верно.
Что и требовалось доказать.
б) Пусть первое число равно x, тогда второе число равно x+1.
(x-x+1)^2+4x(x+1)=(x+x+1)^2
1+4x^2+4x=(2x+1)^2
4x^2+4x+1=(2x+1)^2
(2x+1)^2=(2x+1)^2 – верно.
Что и требовалось доказать.
в) Пусть первое число равно x, тогда второе число равно x+1.
(x+x+1)^2-4x(x+1)=(x-x+1)^2
(2x+1)^2-4x^2-4x=1^2
4x^2+4x+1-4x^2-4x=1
1=1 – верно.
Что и требовалось доказать.
Популярные решебники 7 класс Все решебники
*размещая тексты в комментариях ниже, вы автоматически соглашаетесь с пользовательским соглашением